Основы программирования — второй семестр 08-09
Содержание
- 1 Файлы
- 1.1 Введение
- 1.2 Классификация файлов
- 1.3 Понятие файловой переменной, файлового указателя
- 1.4 Буферизация в файлах
- 1.5 Подпрограммы для работы с закрытыми файлами
- 1.6 Типичные ошибки ввода-вывода при работе с файлами
- 1.7 Подпрограммы для работы с типизированными файлами
- 1.8 Подпрограммы для работы с текстовыми файлами
- 2 Указатели
- 3 Динамическая память
- 4 Динамические структуры данных
- 5 Рекурсия
- 5.1 Основные определения
- 5.2 Простые примеры использования рекурсии
- 5.3 Графические изображения рекурсивных вызовов
- 5.4 Примеры использования рекурсии
- 5.5 Доказательство завершимости рекурсии
- 5.6 Формы рекурсивных подпрограмм
- 5.7 Примеры плохого и хорошего использования рекурсии
- 5.8 Быстрая сортировка
- 5.9 Генерация всех перестановок
- 5.10 Генерация всех подмножеств
- 5.11 Перебор с возвратом (backtracking)
- 6 Деревья
- 7 АТД — Абстрактные Типы Данных. Классы как реализация АТД
- 8 Наследование
- 8.1 Основные определения
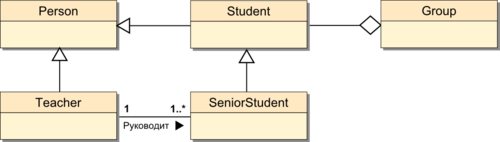
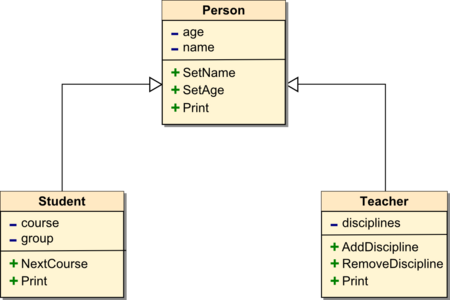
- 8.2 Наследование на примере Student - SeniorStudent
- 8.3 Вызов унаследованных конструкторов
- 8.4 Принцип «открыт - закрыт»
- 8.5 Наследование и включение
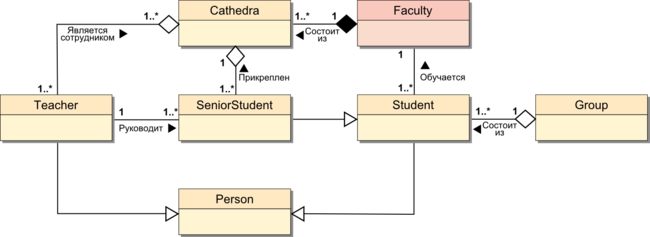
- 8.6 Виды отношений между классами (нотация UML-диаграмм классов)
- 8.7 Вид доступа protected. Рефакторинг метода NextCourse
- 8.8 Наследование и выявление общего предка
- 8.9 Присваивание в иерархии предок-потомок
- 8.10 Операции is и as
- 9 Исключения
- 10 Полиморфизм и виртуальные методы
- 11 Интерфейсы
- 11.1 Реализация интерфейсов
- 11.2 Совместимость по := и операции is as для интерфейсов
- 11.3 Интерфейсы и полиморфизм
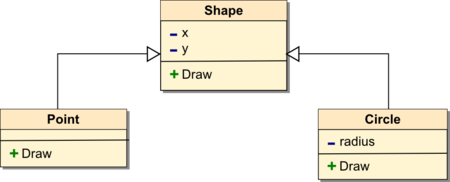
- 11.4 Иерархия графических фигур - классический пример использования полиморфизма
- 11.5 Абстрактные методы и классы
- 11.6 Полиморфные контейнеры
- 11.7 Интерфейсы и наследование
- 11.8 Стандартные интерфейсы .NET
- 11.9 Методы расширения
- 11.10 Методы расширения и интерфейсы
- 11.11 Лямбды
Файлы
Введение
Файл — именованная область на диске, содержащая некоторую информацию.
Преимущества:
- Хранят данные в промежутках между запусками программ.
- Размер данных в файле может существенно превышать оперативную память компьютера.
Классификация файлов
Файлы обычно классифицируют по двум признакам:
1. По типу компонент:
- текстовые;
- двоичные:
- типизированные;
- бестиповые.
2. По способу доступа:
- последовательный;
- произвольный.
Текстовые файлы
Тип text.
Состоят из строк переменной длины, в конце каждой из которых находится символ перехода на новую строку (#13#10 в Windows, #10 в Linux). В PascalABC.NET это константа NewLine.
Двоичные файлы: информация хранится в виде двоичного кода.
Типизированные файлы
Тип file of <type>. Содержат данные фиксированного типа <type>.
Бестиповые файлы
Тип file. Могут хранить данные различных типов.
В двоичных файлах информация хранится в том виде, как она хранится в оперативной памяти, а в текстовых числовая информация преобразуется к строковому виду и обратно, что занимает больше времени.
Файл называется
- файлом произвольного доступа, если можно перейти к его i-му элементу за время, не зависящее от размеров файла («за константное время»),
- файлом последовательного доступа, если переход к i-му элементу требует количество операций, пропорциональное i («требует линейного времени»).
Все файлы, содержащие элементы разного размера могут иметь только последовательный доступ к элементам. Таковыми являются:
- текстовые,
- бестиповые файлы.
Типизированные файлы имеют произвольный доступ.
Понятие файловой переменной, файлового указателя
Перед тем, как работать с информацией в файле, его надо открыть.
После этого можно выполнять операции чтения из файла и записи в файл.
По окончании работы его нужно закрыть.
Закрытый файл можно:
- переименовывать
- перемещать
- копировать
- удалять
С каждым открытым файлом связан так называемый файловый указатель, который указывает на текущую позицию в файле.
Файловый указатель создается при открытии файла, и, как правило, устанавливается на 1й элемент файла.
После каждой операции чтения или записи файловый указатель продвигается вперед на размер считанных элементов.
Паскаль-программа
var f: file of integer;
begin
Assign(f, 'a.dat');
{связывает файловую переменную f с файлом на диске 'a.dat'
(файл на диске может отсутствовать)}
//файл состоит из элементов (1, 2, 3)
Reset(f); //файловый указатель — на элемент "1"
var x: integer;
read(f, x); //x = 1
//файловый указатель — на элемент "2"
write(f, x + 4, 666); //теперь файл состоит из элементов (1, 5, 666)
//файловый указатель — за концом файла
{выполнить read(f, x) НЕЛЬЗЯ, т.к. произойдет
ошибка времени выполнения
"чтение за концом файла"}
write(f, 777); //можно
Close(f);
end.2 способа открытия файла
- Reset(f) — открытие текстового файла на чтение, а двоичного — на чтение и запись;
файл должен существовать;
файловый указатель — на начало файла; - Rewrite(f) — создание нового файла (если такого файла не существовало) или обнуление существующего;
файловый указатель — в начало;
текстовые файлы при этом открываются только на запись, а двоичные — на чтение и запись;
Функция Eof(f) [расшифровывается как End Of File] возвращает true, если файловый указатель находился за концом файла.
После работы с данными в файле его необходимо закрыть с помощью Close(f).
Если, не закрывая, выполнить Reset(f), то файловый указатель просто перейдет к началу.
Буферизация в файлах
С каждым файлом связан некий буфер памяти, в который информация из файла частично считывается, и, из которого записывается в нужную часть файла.
Наличие буфера ускоряет операции чтения и записи, поскольку они выполняются преимущественно не с внешним устройством (файлом), а с участком оперативной памяти.
Если забыть закрыть файл, открытый на запись, то можно потерять лишь данные, сохраненные в буфере.
Подпрограммы для работы с закрытыми файлами
procedure Rename(f, name);
//переименовывает файл, связанyый с файловой переменной f, давая ему имя name
procedure Erase(f);
//удаляет файл, связанный с файловой переменной f
function FileExists(name): boolean;
//возвращает True, если файл с именем name существует
function DeleteFile(name): boolean;
//удаляет файл. Если файл не может быть удален, то возвращает False
function RemoveDir(name): boolean;
//удаляет каталог. Возвращает True, если каталог успешно удален
function GetCurrentDir: string;
//возвращает текущий каталог
function SetCurrentDir(name): boolean;
//устанавивает текущий каталог. Возвращает True, если каталог успешно установлен
function CreateDir(name): boolean;
//создает каталог. Возвращает True, если каталог успешно создан
function ExtractFileName(name): string;
//выделяет имя файла из полного имени файла name
function ExtractFileExt(name): string;
//выделяет расширение из полного имени файла name
function ExtractFilePath(name): string;
//выделяет путь из полного имени файла name
Типичные ошибки ввода-вывода при работе с файлами
- Файл открыли, но забыли выполнить Assign.
- Открыли, но файла нет на диске (или нет прав доступа на чтение).
- Попытка считывания за концом файла.
Все эти ошибки нужно обрабатывать с помощью исключений.
Пример 1. Файл не существует.
Assign(f, 'a.dat');
try
Reset(f);
read(f, x);
Close(f);
except
writeln('Файл не существует');
end;Оператор try..finally
try <действия, которые могут вызвать исключение> finally <действия, которые надо выполнить независимо от того, произошло исключение, или нет> end;
Этот оператор отличается тем, что не обрабатывает исключение, а лишь выполняет некоторое завершающее действие, которое должно быть совершено в любом случае. Для обработки нужен внешний блок try..except.
Пример 2. Попытка считывания за концом файла.
Assign(f, 'a.dat');
try
Reset(f);
try
read(f, x);
finally
Close(f);
end;
except
writeln('Произошла ошибка ввода-вывода');
end;Подпрограммы для работы с типизированными файлами
procedure Truncate(f)
//Усекает типизированный файл f, отбрасывая все элементы с позиции файлового указателя
function FileSize(f)
//Возвращает количество элементов в типизированном файле f
function FilePos(f)
//Возвращает текущую позицию файлового указателя в типизированном файле f
procedure Seek(f, i);
//Устанавливает текущую позицию файлового указателя в типизированном файле f на элемент с номером i
Варианты использования
- Перейти на конец файла для добавления элементов:
Seek(f, FileSize(f));
- Перейти на предыдущую позицию:
Seek(f, FilePos(f) - 1);
Пример 1. Добавить в конец файла 'a.dat' элемент 0 (при необходимости создать файл).
const
fileName = 'a.dat';
var
f: file of integer;
begin
Assign(f, fileName);
if FileExists(fileName) then
begin
Reset(f);
Seek(f, FileSize(f));
end
else
Rewrite(f);
write(f, 0);
Close(f);
end.Пример 2. Возведение всех элементов файла в квадрат.
const
fileName = 'a.dat';
var
f: file of real;
begin
Assign(f, fileName);
Reset(f);
for var i:=0 to FileSize(f)-1 do
begin
var x: real;
read(f, x);
Seek(f, i);
write(f, x * x);
end;
Close(f);
end.Пример 3. Использование типизированных файлов для работы с простейшими БД.
БД студентов 1.9
Опишем запись для одного студента:
type
Student = record
name: string[50];
course, group: integer;
end;Замечание. В связи с тем, что типизированные файлы хранят данные фиксированного размера, а string — переменной длины, использовать его в типизированных файлах мы не можем. Для этого будем использовать строки фиксированной длины — string[n] (строка длины n).
Пусть уже создан файл 'Group1course.dat'.
Задача. Найти Иванова и перевести его в 8 группу.
type
Student = record
name: string[50];
course, group: integer;
end;
const
fileName = 'a.dat';
var
f: file of Student;
begin
Assign(f, fileName);
Reset(f);
while not Eof(f) do
begin
var x: Student;
read(f, x);
if (x.name = 'Иванов') and (x.group = 11) then
begin
x.group := 10;
Seek(f, FilePos(f) - 1);
write(f, x);
break;
end;
end;
Close(f);
end.Пример 4. Сортировка файла по возрастанию.
for var i:=FileSize(f)-2 downto 0 do
for var j:=0 to i do
begin
Seek(f,j);
read(f,x,y);
if x>y then
begin
Seek(f,j);
write(f,y,x);
end;
end;Подпрограммы для работы с текстовыми файлами
procedure Reset(f)
//Открывает текстовый файл f ТОЛЬКО на чтение.
procedure Rewrite(f)
//Открывает текстовый файл f ТОЛЬКО на запись, обнуляя его содержимое
procedure Append(f)
//Открывает текстовый файл f на дополнение
//Файловый указатель устанавливается за концом файла
function Eoln(f)
//Возвращает True, если файловый указатель находится на символе конца строки в текстовом файле f
function SeekEof(f)
//Пропускает пробельные символы, после чего возвращает True, если достигнут конец текстового файла f
function SeekEoln(f)
//Пропускает пробельные символы, после чего возвращает True, если достигнут конец строки в текстовом файле f
procedure read(f, a, b, c)
//Считывает значения в переменные a, b, c;
//Переменные могут быть числовых типов, символьного, строкового
procedure write(f, a, b, c)
//Записывает значения переменных a, b, c в текстовый файл f;
//Переменные могут быть числовых типов, символьного, строкового
procedure readln(f, a, b, c);
procedure writeln(f, a, b, c);
procedure readln(f);
procedure writeln(f);
Примеры использования
Пример 1. Обработка строк в текстовых файлах.
Пусть имеется функция, которая трансформирует строку и возвращает string:
function Transform(var s: string): string;
Применить указанную трансформацию ко всем строкам файла.
var
f, f1: text;
begin
Assign(f, 'a.txt');
Assign(f1, 'b$.txt');
Reset(f);
Rewrite(f1);
while not Eof(f) do
begin
var s: string;
readln(f, s); //Важно использовать readLN, т.к. она пропускает символы перехода
//на новую строку (если использолвать read, произойдет зацикливание)
s := Transform(s);
writeln(f1, s);
end;
Close(f);
Close(f1);
Erase(f);
Rename(f1, 'a.txt');
end.Пример 2. Сумма целых в текстовом файле.
var f: text;
begin
var sum := 0.0;
assign(f,'a.txt');
reset(f);
while not SeekEof(f) do
begin
var x: real;
read(f,x);
sum += x;
end;
close(f);
writeln(sum);
end..NET-типы File и Directory и их статические методы
uses System.IO, System.Text;
begin
&File.Copy('p1.pas','p2.pas',true);
&File.Exists('p2.pas');
var s: string := &File.ReadAllText('p1.pas');
var s1: string := &File.ReadAllText('p1.pas',Encoding.Default);
var ss: array of string := &File.ReadAllLines('p1.pas');
&File.WriteAllLines('p3.pas',ss);
&File.WriteAllText('p4.pas',s);
&File.AppendAllText('p2.pas',s);
&File.Move('p3.pas','p5.pas');
&File.Delete('p5.pas');
Directory.GetCurrentDirectory();
Directory.SetCurrentDirectory('d:\w');
var fnames: array of string := Directory.GetFiles('.');
var dnames: array of string := Directory.GetDirectories('..');
Directory.Exists('d:\w');
end.Указатели
Адрес
Оперативная память состоит из последовательный ячеек. Каждая ячейка имеет номер, называемый адресом.
В 32-битных системах можно адресовать 232 байт (<math>\approx \;</math> 4Гб) памяти, в 64-битных — 2 64 соответственно.
Переменная (или константа), хранящая адрес, называется указателем.
Для чего нужны указатели
Указатели повышают гибкость доступа к данным:
- Вместо самих данных можно хранить указатель на них. Это позволяет хранить данные в одном экземпляре и множество указателей на эти данные. Через разные указатели эти данные можно обновлять (пример — корпоративная БД).
- Указателю можно присвоить адрес другого объекта (вместо старого появился новый телефонный справочник).
- С помощью указателей можно создавать сложные структуры данных.
Типы указателей
Указатели делятся на:
- Типизированные (указывают на объект некоторого типа)
Имеют тип: ^<тип>
Пример. ^integer — указатель на integer - Бестиповые (хранят адрес ячейки памяти неизвестного типа)
Преимущество: могут хранить что угодно
Имеют тип: pointer
Пример кода.
var
i: integer := 5;
r: real := 6.14;
pi: ^integer;
pr: ^real;
begin
pi := @i;
pr := @r;
pi := @r; // ОШИБКА компиляции
end.@ — унарная операция взятия адреса
Операция разадресации (разыменования)
var
i: integer := 5;
pi: ^integer;
begin
pi := @i;
pi^ := 8 - pi^;
writeln(i); // 3
end.^ — операция разыменования
pi^ — то, на что указывает pi, т.е. другое имя i или ссылка на i.
Тут надо вспомнить определение ссылки:
Ссылка — другое имя объекта.
Нулевой указатель
Все глобальные неинициализированные указатели хранят специальное значение nil, что говорит о том, что они никуда не указывают.
Указатель, хранящий значение nil называется нулевым.
var
pi: ^integer; //указатель pi хранит значение nil
i: integer;
begin
pi := @i; //pi хранит адрес переменной i
pi := nil; //pi снова никуда не указывает
pi^ := 7; //ОШИБКА времени выполнения:
//попытка разыменовать нулевой указательПопытка разыменовать нулевой указатель приводит к ошибке времени выполнения.
Бестиповые указатели
var
p: pointer;
i: integer;
begin
p := @i;
end.Бестиповому указателю можно присвоить адрес переменной любого типа, т.е. бестиповой указатель совместим по присваиванию с любым типовым указателем.
Попытка разыменовать бестиповой указатель приводит к ошибке компиляции. Т.е. он может только хранить адреса.
Оказывается, любой типизированный указатель совместим по присваиванию с бестиповым, т.е. следующий код верен:
var
pi: ^integer;
i: integer;
p: pointer;
begin
p := @i;
pi := p;
pi^ += 2;
end.Вопрос. Нельзя ли интерпретировать память, на которую указывает p, как принадлежащую к определенному типу?
Ответ — да, можно. Вот как это сделать:
type
pinteger = ^integer;
var
i, j: integer;
p: pointer;
begin
p := @i;
pinteger(p)^ := 7; //используем явное приведение типа
writeln(i); // 7
end.Запись
тип(переменная)
показывает, что используется явное приведение типов.
Внимание! Неконтролируемая ошибка!
type
preal = ^real;
var
i, j: integer;
p: pointer;
begin
p := @i;
preal(p)^ := 3.14; //ОШИБКА!
end.Область памяти, на которую указывает p трактуется как область, хранящее вещественное число (8 байт), и потому константа 3.14 записывается в эти 8 байт. Однако, переменная i занимает только 4 байта, поэтому затираются еще 4 соседних байта (в данном случае они принадлежат переменной j).
Доступ к памяти, имеющей другое внутреннее представление
type
Rec = record
b1, b2, b3, b4, b5, b6, b7, b8: byte;
end;
PRecord = ^Rec;
var
r: real := 3.1415;
prec: ^Rec;
begin
var temp : pointer := @r;
prec := temp;
writeln(prec^.b1, ' ', prec^.b2, ' ', {..., } prec^.b8);
end.Замечание. Важно, что типы real и Rec имеют один размер.
Другой способ сделать то же самое, но гораздо более безопасный - использовать класс System.BitConverter
uses System;
begin
foreach b: byte in BitConverter.GetBytes(1.0) do
write(b,' ');
end.Неявные указатели в языке Pascal
- procedure p(var i: integer)
Для параметра-переменной при вызове на стек кладется не сама переменная, а указатель на неё. - var pp: procedure(i: integer)
Для хранения процедурной переменной используется ячейка памяти, являющаяся указателем. - var a: array of real;
Переменная типа динамический массив является указателем на данные массива, хранящиеся в динамической памяти.
Динамическая память
Особенности динамической памяти
Память, принадлежащая программе, делится на:
- Статическую
(память, занимаемая глобальными переменными и константами) - Автоматическую
(память, занимаемая локальными данными, т.е. стек программы) - Динамическую
(память, выделяемая программе по специальному запросу)
В дополнение к статической и автоматической памяти, которые фиксированы после запуска программы, программа может получать нефиксированное количество динамической памяти. Ограничения на объём выделяемой динамической памяти связаны лишь с настройками операционной системы и объемом оперативной памяти компьютера.
Основная проблема — явно выделенную динамическую память необходимо возвращать, иначе не хватит памяти другим программам.
Для явного выделения и освобождения динамической памяти используются процедуры:
- New
- Dispose
var
p: pinteger; //p никуда не указывает
begin
New(p); //в динамической памяти выделяется ячейка
//размером под один integer, и
//p начинает указывать на эту ячейку
p^ := 3;
Dispose(p); //возвращает динамическую память,
//контролируемую указателем p, назад ОС
end.По окончании работы программы, вся затребованная программой динамическая память возвращается ОС.
Но лучше освобождать динамическую память явно! Иначе в процессе работы программы она может занимать большие объёмы (ещё не освобождённой) памяти, что вредит общей производительности системы.
Ошибки при работе с динамической памятью
1.var p: pinteger;
begin
p^ := 5; //ОШИБКА
end.Ошибка разыменования нулевого указателя (попытка использовать невыделенную динамическую память).
2.var p: pinteger;
begin
New(p);
New(p); //ОШИБКА
end.Утечка памяти (память, которая выделилась в результате первого вызова New(p), принадлежит программе, но не контролируется никаким указателем.
2a.procedure q;
var p: pinteger;
begin
New(p);
end;
begin
q; //ОШИБКА
end.Утечка памяти в подпрограмме: обычно если динамическая память выделяется в подпрограмме, то она должна в этой же подпрограмме возвращаться. Исключение составляют т.н. "создающие" п/п:
function CreateInteger: pinteger;
begin
New(Result);
end;
begin
var p: pinteger := CreateInteger;
p^ := 555;
Dispose(p);
end.Ответственность за удаление памяти, выделенной в подпрограмме, лежит на программисте, вызвавшем эту подпрограмму.
3.var p: pinteger;
begin
for var i:=1 to 1000000 do
New(p); //ОШИБКА
end.Out of Memory (очень большие утечки памяти, в результате которых динамическая память может «исчерпаться»).
4.var p: pinteger;
begin
New(p);
p^ := 5;
Dispose(p);
p^ := 7; //ОШИБКА
end.После вызова Dispose(p), p называют висячим указателем (т.к. он указывает на недоступную более область памяти).
Динамические структуры данных
Введение
Данные объединяются в структуры.
Мы уже знаем такие структуры данных как:
- массивы (подразумеваем статические)
- записи
Их основная проблема — фиксированный размер, определяемый на этапе компиляции.
Решением проблемы являются динамические структуры данных. Они строятся из узлов, которые, в свою очередь, состоят из данных и полей связи.
Рассмотрим такой пример:
type
Node<DataType> = class
data: DataType;
next: Node<DataType>;
constructor (d: DataType; n: Node<DataType>);
begin
data := d;
next := n;
end;
end;
begin
var p := new Node<char>('!', nil); // под объект класса Node<char> выделилась динамическая память;
// p начала указывать на эту динамическую память
end.Виды списков
- Линейный односвязный список

- Циклический односвязный список

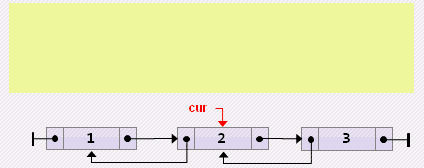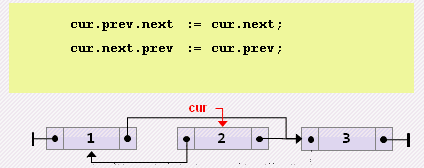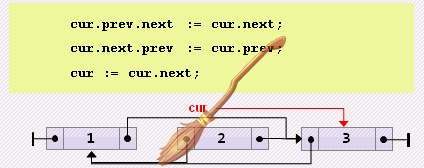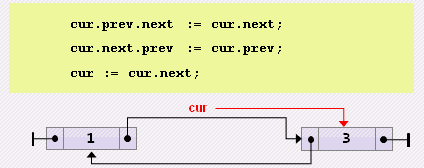
- Двусвязный линейный список

- Циклический двусвязный список
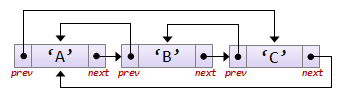
Односвязные линейные списки
Класс узла односвязного списка
/// <summary>
/// Узел односвязного линейного списка
/// </summary>
type SNode<T> = class
public // <- для печати write
/// Поле данных
data: T;
/// Поле связи со следующим узлом
next: SNode<T>;
/// <summary>
/// Инициализирует новый экземпляр узла односвязного списка
/// со значением dt поля данных и ссылкой next на следующий узел
/// </summary>
/// <param name="dt">Значение поля данных узла</param>
/// <param name="next">Сслыка на следующий узел. По умолчанию: nil</param>
constructor(dt: T; next: SNode<T> := nil);
begin
data := dt;
self.next := next;
end;
end;
/// Умный конструктор типа SNode: вывод типа и экономия на слове new
function MkSnode<T>(dt: T; next: SNode<T> := nil) := new SNode<T>(dt, next);Стандартные операции с односвязными линейными списками
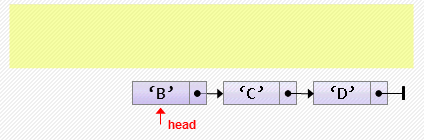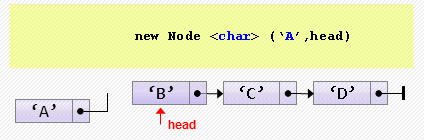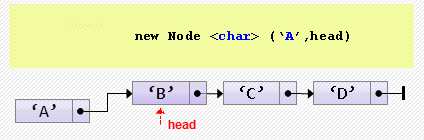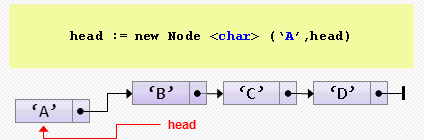
- Вставка элемента в начало
head := new Node<char>('A', head);При многократной вставке в начало элементы располагаются в обратном порядке.
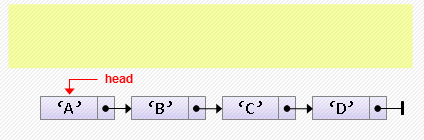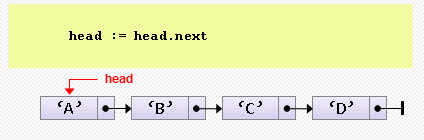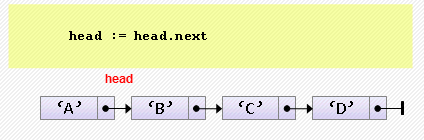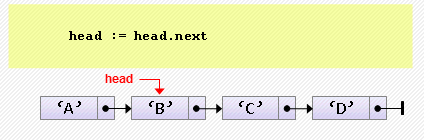
- Удаление элемента из начала
head := head.next;Если изначально список пуст, произойдет ошибка «попытка разыменования нулевого указателя». Эту ситуацию надо предусмотреть:
if head <> nil then
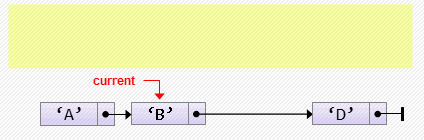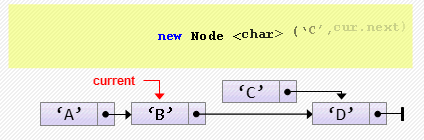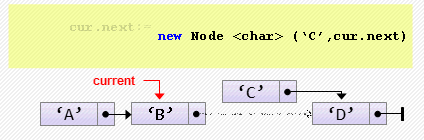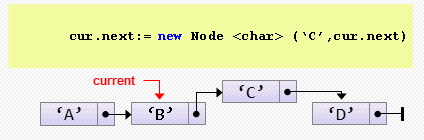
head := head.next;- Вставка элемента после текущего
cur.next := new Node<char>('C', cur.next);Если cur никуда не указывает, произойдет ошибка. Предусмотрим эту ситуацию:
if cur <> nil then
cur.next := new Node<char>('d', cur.next);Заметим также, что если cur указывает на последний элемент списка, ошибки не произойдет (фактически, будет произведена вставка в конец списка).
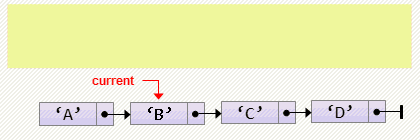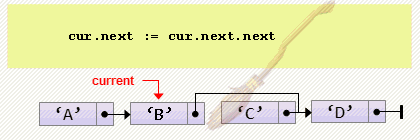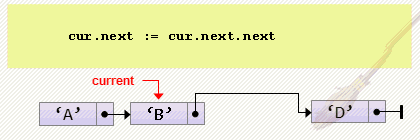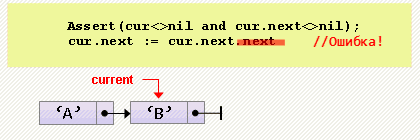
- Удаление элемента после текущего
cur.next := cur.next.next;Заметим, что текущий элемент — cur, должен не только не быть пустым, но и не быть последним в списке, т.к. происходят два разыменования: cur.next и cur.next.next. Для проверки этого факта можем воспользоваться утверждением:
Assert( (cur <> nil) and (cur.next <> nil) );
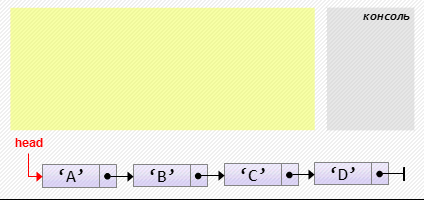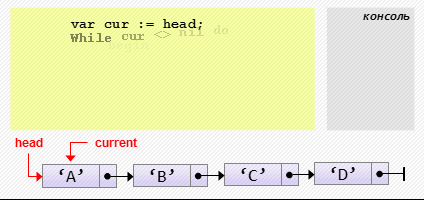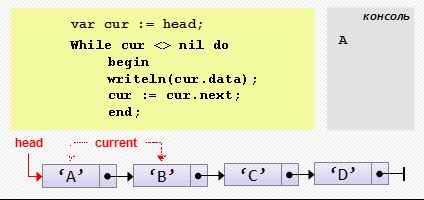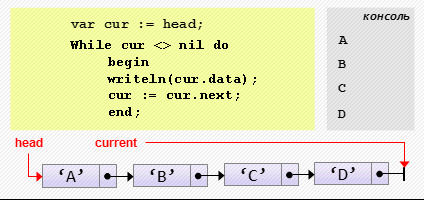
cur.next := cur.next.next;- Проход по списку
var cur := head;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.next;
end;Примеры использования
Пример 1.
Дан файл целых чисел.
Записать все его элементы в линейный односвязный список.
var f: file of integer;
Assign(f, 'numbers.dat');
Reset(f);
var a: integer;
Read(f, a);
var head := new Node<integer>(a, nil);
var cur := head;
while not Eof(f) do
begin
read(f, a);
cur.next := new Node<integer>(a, nil);
cur := cur.next;
end;
Close(f);Пример 2.
Поиск элемента с заданным значением.
// x — искомый символ
var cur := head;
while (cur <> nil) and (cur.data <> x) do
cur := cur.next;
if cur = nil then
// не найдено
else
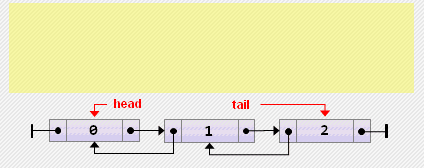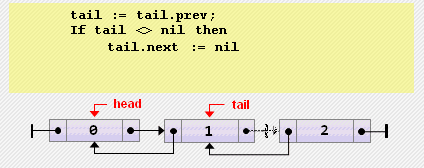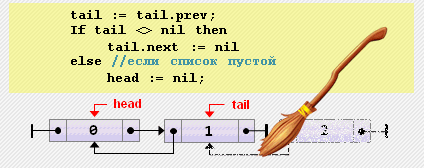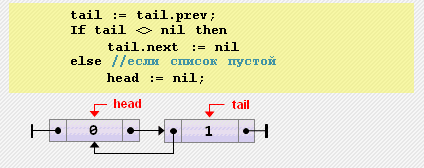
// cur — ссылка на искомый xДвусвязные линейные списки
Класс узла двусвязного списка
В отличие от односвязных линейных списков, двусвязные, помимо полей data и next, имеют поле prev (указатель на предыдущий элемент списка):
type
Node<T> = class
data: T;
prev, next: Node<T>;
constructor (d: T; p, n: Node<T>);
begin
data := d;
prev := p;
next := n;
end;
end;В случае двусвязного списка нам достаточно иметь ссылку на любой узел, тогда все остальные можно найти. Однако, для удобства, будем считать, что у нас есть две ссылки:
- head — на начало списка
- tail — на конец списка
Стандартные операции с двусвязными линейными списками
Замечание. При выполнении любой операции нужно следить за возможными изменениями head и tail.
- Инициализация
head := nil;
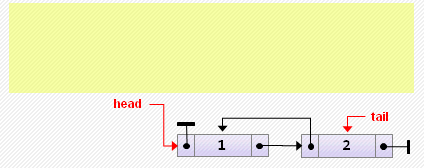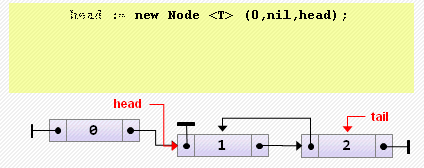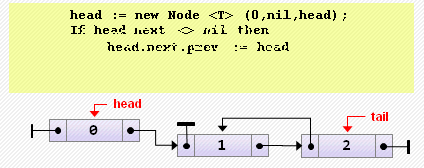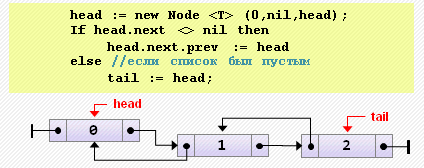
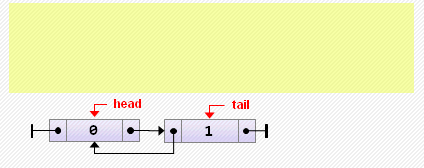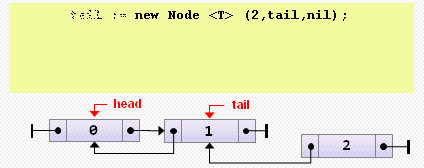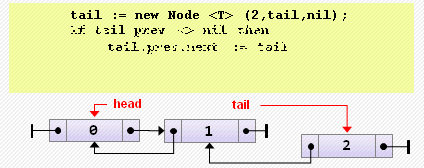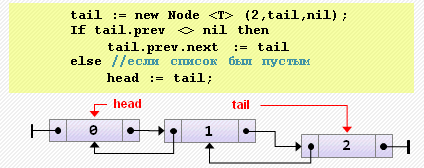
tail := nil;- Добавление элемента в начало
Примечание. Если изначально список был пуст, после добавления элемента надо не забыть сделать tail указывающим на него.
head := new Node<T>(0, nil, head);
if head.next <> nil then
head.next.prev := head
else // если список был пуст
tail := head;- Добавление элемента в конец
tail := new Node<T>(2, tail, nil);
if tail.prev <> nil then
tail.prev.next := tail
else // если список был пуст
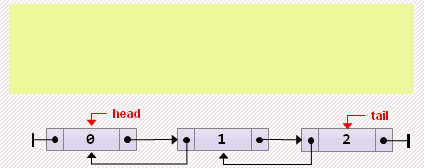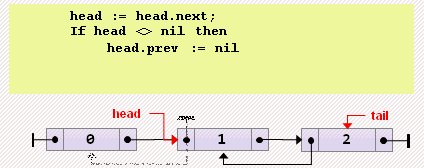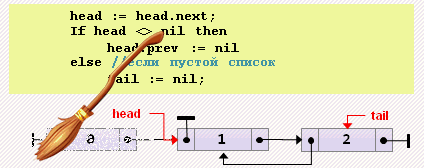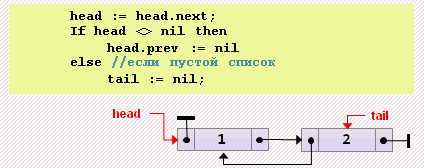
head := tail;- Удаление элемента из начала
head := head.next;
if head = nil then
tail := nil
else
head.prev := nil;- Удаление элемента из конца
tail := tail.prev;
if tail = nil then
head := nil
else
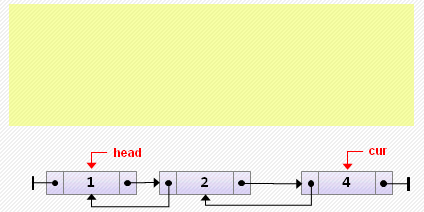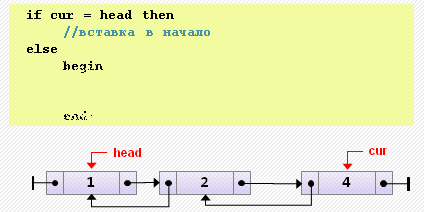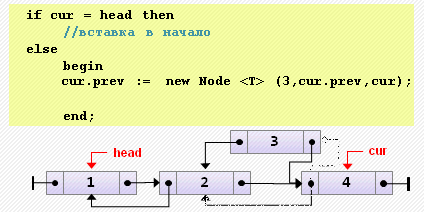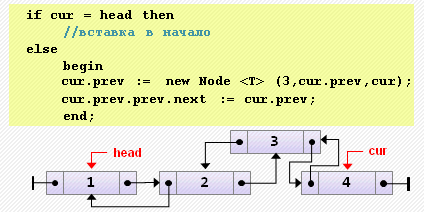
tail.next := nil;- Вставка элемента перед текущим
if cur = head then
// вставка в начало
else
begin
cur.prev := new Node<T>(3, cur.prev, cur);
cur.prev.prev.next := cur.prev;
end;- Вставка элемента после текущего
if cur = tail then
// вставка в конец
else
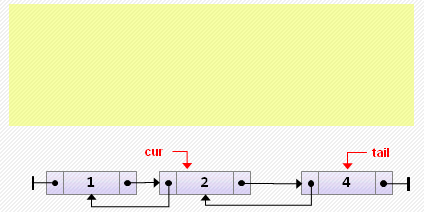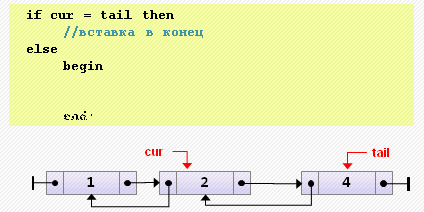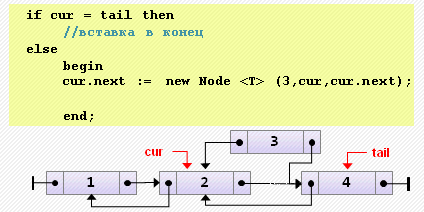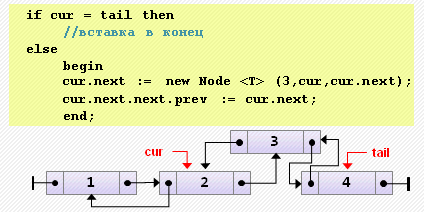
begin
cur.next := new Node<T>(3, cur, cur.next);
cur.next.next.prev := cur.next;
end;- Удаление текущего
if cur = head then
// удаление из начала
else if cur = tail then
// удаление из конца
else
begin
cur.prev.next := cur.next;
cur.next.prev := cur.prev;
cur := cur.next;
end;- Проход по списку
Проход по списку в прямом порядке аналогичен этой операции для односвязных списков.
Проход в обратном порядке можно организовать заменой:
- head на tail
- next на prev
Класс двусвязного линейного списка - устарело, на лекции не даю - громоздко и надо пользоваться стандартным
Ясно, что удобно оформить все операции в виде подпрограмм. Но тогда каждый раз в качестве параметров надо передавать ссылки на начало и конец списка.
Создадим класс двусвязный линейный список, полями которого будут head и tail:
type
Node<T> = class
data: T;
prev, next: Node<T>;
constructor (d: T; p, n: Node<T>);
begin
data := d;
prev := p;
next := n;
end;
end;
DoubleLinkedList<T> = class
head, tail: Node<T>;
constructor;
begin
head := nil;
tail := nil;
end;
procedure AddFirst(d: T);
begin
head := new Node<T>(d, nil, head);
if head.next <> nil then
head.next.prev := head
else // если список был пуст
tail := head;
end;
procedure AddLast(d: T);
begin
tail := new Node<T>(d, tail, nil);
if tail.prev <> nil then
tail.prev.next := tail
else // если список был пуст
head := tail;
end;
procedure DeleteFirst;
begin
head := head.next;
if head = nil then
tail := nil
else
head.prev := nil;
end;
procedure DeleteLast;
begin
tail := tail.prev;
if tail = nil then
head := nil
else
tail.next := nil;
end;
procedure InsertBefore(cur: Node<T>; d: T);
begin
if cur = head then
AddFirst(d)
else
begin
cur.prev := new Node<T>(d, cur.prev, cur);
cur.prev.prev.next := cur.prev;
end;
end;
procedure InsertAfter(cur: Node<T>; d: T);
begin
if cur = tail then
AddLast(d)
else
begin
cur.next := new Node<T>(d, cur, cur.next);
cur.next.next.prev := cur.next;
end;
end;
function RemoveAt(cur: Node<T>): Node<T>;
begin
if cur = head then
begin
DeleteFirst;
Result:=head;
end
else if cur = tail then
begin
DeleteLast;
Result:=nil;
end
else if cur = tail then
begin
DeleteLast;
result := nil;
end
else
begin
cur.prev.next := cur.next;
cur.next.prev := cur.prev;
result := cur.next;
end;
end;
procedure Print;
begin
var cur := head;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.next;
end;
end;
procedure PrintReverse;
begin
var cur := tail;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.prev;
end;
end;
end;Пример.
Дан двусвязный линейный список с целыми значениями.
Удалить все его отрицательные элементы.
var list: DoublyLinkedList<integer>;
// создание списка
var cur := list.head;
while cur <> nil do
if cur.data < 0 then
cur := list.RemoveAt(cur)
else
cur := cur.next;Сравнение списков и массивов
по количеству операция (n - кол-во элементов)
| Массив | Список | |
|---|---|---|
| Вставка в конец, удаление из конца | <math>\Theta (1)</math> | <math>\Theta (1)</math> |
| Вставка в начало, удаление из начала | <math>\Theta (n)</math> | <math>\Theta (1)</math> |
| Вставка в середину, удаление из середины | <math>\Theta (n)</math> | <math>\Theta (1)</math> |
| Проход | <math>\Theta (n)</math> | <math>\Theta (n)</math> |
| Доступ по индексу | <math>\Theta (1)</math> | <math>\Theta (i)</math> |
| Поиск | <math>\Theta (n)</math> | <math>\Theta (n)</math> |
Рекурсия
Основные определения
Рекурсией называется определение объекта через такой же объект.
Пример.
(1) <Список> ::= <Число>
|<Список> ',' <Число>
В данном примере рекурсивной частью определения является "<Список> ',' <Число>".
Замечание 1. Рекурсивное определение, будучи конечным, определяет бесконечное множество объектов.
Заметим также, что <Список> можно определить и по-другому:
(2) <Список> ::= <Число>
|<Число> ',' <Список>
Определение (1) называют леворекурсивным, а (2) — праворекурсивным.
Замечание 2. В рекурсивном определении обязательно (!!!) должна присутствовать нерекурсивная часть.
Рекурсивное определение может быть косвенным:
- по одной из ветвей рекурсивного определения упоминается объект, в определении которого, в свою очередь, по одной из ветвей определяется исходный объект.
Пример.
<оператор> ::= <присваивание> | <составной оператор> <присваивание> ::= <переменная> := <выражение> <составной оператор> ::= begin <список операторов> end <список операторов> ::= <пусто> | <оператор> ; <список операторов>
В данном примере имеется как прямое, так и косвенное рекурсивное определение.
В программировании под рекурсией понимается:
- вызов из подпрограммы самой себя (прямая рекурсия)
- вызов из подпрограммы другой подпрограммы, которая вызывает исходную (косвенная рекурсия)
При косвенной рекурсии обязательно использование опережающего объявления с помощью ключевого слова forward:
procedure q; forward; // опережающее определение
procedure p;
begin
...
q;
...
end;
procedure q;
begin
...
p;
...
end;Простые примеры использования рекурсии
Пример 1.
procedure p(i: integer);
begin
write(i, ' ');
p(i + 1);
end;При вызове этой процедуры произойдет рекурсивное зацикливание, т.к. рекурсивный вызов производится безусловно.
Вывод. Чтобы рекурсивного зацикливания не произошло, рекурсивный вызов должен происходить не безусловно, а по какому-то условию, которое всякий раз меняется и при каком-то рекурсивном вызове становится ложным (так называемое условие продолжения рекурсии).
Исправим нашу процедуру в соответствии со сделанным выводом:
procedure p(i: integer);
begin
write(i, ' ');
if i < 5 then
p(i + 1);
end;При вызове p(0) будет выведено:
0 1 2 3 4 5
Графически, рекурсивные вызовы можно изобразить так:

Процесс последовательных рекурсивных вызовов подпрограммы из самой себя называется рекурсивным спуском.
Процесс возврата из рекурсивных вызовов называется рекурсивным возвратом.
В данном примере числа выводятся на рекурсивном спуске (т.е. в прямом порядке).
Однако, чтобы действия выполнялись в обратном порядке, их нужно вызывать на рекурсивном возврате.
Пример 2. Вывести
0 1 2 3 4 5 4 3 2 1 0
Решение:
procedure p(i: integer);
begin
write(i, ' ');
if i < 5 then then
begin
p(i + 1);
write(i, ' ');
end;
end;Максимальная глубина рекурсивных вызовов называется глубиной рекурсии.
Текущая глубина называется текущим уровнем рекурсии.
Замечание. Чем больше глубина рекурсии, тем больше накладные расходы по памяти.
Графические изображения рекурсивных вызовов
Одно графическое изображение у нас уже было. Вспомним его:
procedure p(i: integer);
begin
write(i, ' ');
if i < 5 then
p(i + 1);
end;Рассмотрим более детально вызов p(0) процедуры
procedure p(i: integer);
begin
write(i, ' ');
if i < 2 then
p(i + 1);
end;Вспомним, что:
- Программный стек — это непрерывная область памяти, выделяемая программе, в частности, для размещения в ней вызываемых подпрограмм.
- При каждом вызове подпрограммы на стек кладется её запись активации (ЗА), а при возврате — снимается со стека.

Т.о. на стеке фактически хранятся все значения переменной i.
Замечание 1. Поскольку при каждом рекурсивном вызове на стек помещается ЗА, то при большой глубине рекурсии программный стек может переполниться, и программа завершится с ошибкой.
Это произойдет тем быстрее, чем больше суммарный объем формальных параметров и локальных переменных.
Поэтому следующий код — очень плохой!!!
procedure p(i: integer);
var a : array[1..1000] of real;
begin
...
p(i + 1);
...
end;Замечание 2. Накладные расходы на помещение на стек ЗА, снятие ЗА со стека, а также присваивание значений формальным параметрам на стеке достаточно велики.
Поэтому если имеется простое нерекурсивное решение (итерационное), то следует использовать именно его.
Замечание 3. Любую рекурсию можно заменить итерацией.
Примеры использования рекурсии
Пример 1. Найти n! = n(n - 1)(n - 2)...2*1
Очевидно, определить n! можем следующим образом:
- <math>f(n) = \begin{cases} n (n - 1), & n > 0 \\ 1, & n = 0 \end{cases}</math>
Тогда решение имеет вид:
function nfact(n: integer): integer;
begin
if n = 0 then
Result := 1
else
Result := n * nfact(n - 1);
end;Однако, заметим, что возвращаемое значение не определено для n < 0.
Как минимум, можно заменить условие n = 0 на n <= 0, но, в таком случае, мы получим неверный результат, т.к. факториал вообще не определен для отрицательных чисел.
Очевидно, необходимо с помощью утверждения проверить корректность входного параметра (Assert(n >= 0)). Но его использование при каждом рекурсивном вызове накладно. Поэтому можно "обернуть" рекурсивную подпрограмму, например, так:
function nfact(n: integer): integer;
function nfactRecur(n: integer): integer;
begin
if n = 0 then
Result := 1
else
Result := n * nfact(n - 1);
end;
begin
Assert(n >= 0);
Result := nfactRecur(n);
end;Глубина рекурсии этого алгоритма равна n.
Пример 2. Найти <math>a^n</math>.
Дадим рекурсивное определение:
- <math>f(n) = \begin{cases} (a^{\frac{n}{2}})^2, & \mbox{if }n\mbox{ is even}, n > 0
\\ a a^{n-1}, & \mbox{if }n\mbox{ is odd}, n > 0 \\ 1, & n = 0 \\ \frac{1}{a^n}, & n < 0\end{cases}</math>
function power(a: real; n: integer): real;
begin
if n = 0 then
Result := 1
else if n < 0 then
Result := 1 / power(a, -n)
else // n > 0
if n mod 2 = 0 then
Result := sqr(power(a, n div 2))
else
Result := a * power(a, n - 1);
end;Глубина рекурсии равна:
- <math>\log_2 n</math> — в лучшем случае
- <math>2\log_2 n</math> — в худшем
Пример 3. Нахождение минимального элемента в массиве.
Определить этот элемент можем как минимальный(один элемент, минимальный из массива без этого элемента), т.е. рекурсивное определение следующее:
- <math>minElem(A, n) = \begin{cases} A[n-1], & n = 1
\\ min(\; minElem(A, \; n - 1),\; A[n - 1]\;), & n > 1\end{cases}</math> В соответствии с этим имеем решение:
function MinElem(A: array of integer; n: integer): integer;
begin
if n = 1 then
Result := A[0]
else
Result := min(MinElem(A, n-1), A[n-1]));
end;Глубина рекурсии равна n - 1.
Ясно, что это не очень хороший результат.
Можно значительно уменьшить глубину, если искать минимальный среди примерно равных частей массива.
Т.е. нужно поделить массив пополам, найти в каждой половине минимальные элементы и сравнить их. Поиск в половине осуществляется подобным же образом, и деление производится до тех пор, пока в подмассиве не останется один элемент.
Можно еще немного оптимизировать этот алгоритм — если в подмассиве два элемента, достаточно вернуть минимальный из них.
Теперь знания количества элементов недостаточно: необходимо знать, среди каких элементов массива вести поиск. Поэтому будем в качестве параметров передавать левую (l) и правую (r) границы подмассивов.
Дадим новое рекурсивное определение:
- <math>minElem(A, l, r) = \begin{cases} A[l], & l = r
\\ min(A[l],\; A[r]), & r - l = 1 \\ min(\; minElem(A,\; l, \; (l + r) \; div\; 2), \; minElem( A, \; (l + r)\; div\; 2 + 1,\; r) \;), & l - r > 1\end{cases}</math> Решение:
function MinElem(a: array of integer; l, r: integer): integer;
begin
if l = r then // если всего один элемент
Result := a[l]
else if r - l = 1 then // если ищем минимум из двух элементов
Result := min(a[l], a[r])
else
begin
var mid := (l + r) div 2;
Result := min(MinElem(a, l, mid), MinElem(a, mid+1, r));
end;
end;Глубина рекурсии такого алгоритма уже примерно равна <math>\log_2 n</math> (по количеству делений).
Пример 4. Вывод односвязного линейного списка на экран.
Вспомним, как выглядит список:
![]()
Решение:
procedure Print<T>(h: Node<T>);
begin
if h = nil then
exit;
write(h.data, ' ');
Print(h.next);
end;Глубина рекурсии равна длина списка - 1
Рекурсия называется концевой, если рекурсивный вызов является последним в подпрограмме.
Концевая рекурсия наиболее легко превращается в итеративный алгоритм:
while h <> nil do
begin
write(h.data, ' ');
h := h.next;
end;Доказательство завершимости рекурсии
Добавим к рекурсивной процедуре целый параметр n:
p(n, ...);
Если при каждом рекурсивном вызове параметр n уменьшается получим вызовы
p(n)
p(n - 1)
p(n - 2)
p(n - 3)
И если рекурсия завершается при n <= 0, то это служит доказательством завершимости рекурсии.
Действительно, на каждом следующем уровне рекурсии n становится меньше.
Поскольку при n <= 0 рекурсивных вызовов нет, то число рекурсивных вызовов конечно.
Утверждать, что рекурсия завершима, можно не всегда.
Пример.
procedure p(n);
begin
if n <= 0 then
exit
else
p(Random(2 * n) - n + 1);
end;Формы рекурсивных подпрограмм
1. Действие выполняется на рекурсивном спуске
p(n)
S(n)
if B(n) then
p(n - 1)
2. Действие выполняется на рекурсивном возврате
p(n)
if B(n) then
p(n - 1)
S(n)
3. Действие выполняется и на рекурсивном спуске и на рекурсивном возврате
p(n)
S1(n)
if B(n) then
p(n - 1)
S2(n)
4. Каскадная рекурсия
p(n)
S(n)
if B1(n) then
p(n - 1)
if B2(n) then
p(n - 1)
Эта рекурсия называется каскадной, т.к. каждый вызов подпрограммы может порождать несколько рекурсивных вызовов (каскад).
5. Удаленная рекурсия:
function f(i: integer): integer;
begin
if B1(n) then
Result := ...
else
Result := f(f(i-1));
end;
Примером удаленной рекурсии служит функция Аккермана:
- <math>A(m,\;n)=\begin{cases}n+1,&m=0;
\\A(m-1,\;1),&m>0,\; n = 0; \\A(m-1,\;A(m,\;n-1)),& m > 0,\; n > 0.\end{cases}</math>
Примеры плохого и хорошего использования рекурсии
<xh4>Пример плохого использования рекурсии - числа Фибоначчи</xh4> Числа Фибоначчи задаются следующим рекуррентным соотношением:
- <math>F_1 = 1,\quad F_2 = 1,\quad F_{n+1} = F_n + F_{n-1} \quad n\in\mathbb{N}.</math>
Мы уже вычисляли их с помощью циклов. Возможно рекурсивное (плохое!) решение:
function Fib(n: integer): integer;
begin
if (n = 1) or (n = 2) then
Result := 1
else
Result := Fib(n - 1) + Fib(n - 2);
end;Вот что произойдет при вызове Fib(7):

дерево рекурсивных вызовов
Как видим, одни и те же числа вычисляются по несколько раз:
- Fib(7): 1
- Fib(6): 1
- Fib(5): 2
- Fib(4): 3
- Fib(3): 5
- Fib(2): 8
Алгоритм можно улучшить, использовав массив, первоначально заполненный нулями.
При первом вычислении fib(n) будем заполнять соответствующий элемент, а при всех последующих — просто обращаться к его значению. Подобная методика называется мемоизацией, т.е. запоминанием промежуточных результатов для исключения их повторного вычисления.
var F: array[1..1000] of integer;
function Fib(n: integer): integer;
begin
if F[n] <> 0 then
Result := F[n]
else if (n = 1) or (n = 2) then
begin
Result := 1;
F[n] := 1;
end
else
begin
Result := Fib(n - 1) + Fib(n - 2);
F[n] := Result;
end;
end;Очевидно, данный способ крайне неэффективен по сравнению с итерационным алгоритмом как по памяти, так и по времени работы. В частности, глубина рекурсии при вычислении n-того числа Фибоначчи составляет n-1.
Рекурсивный способ вычисления чисел Фибоначчи, построенный по итерационному алгоритму
Напомним итерационный алгоритм поиска n-того числа Фибоначчи:
a := 1;
b := 1;
for var i := 3 to n do
begin
c := a + b;
a := b;
b := c;
end;
Result := c;Построим по нему рекурсивный алгоритм, передавая в каждую рекурсивную подпрограмму переменные a,b,c, меняющиеся на каждой итерации цикла. Фактически при каждом рекурсивном вызове мы будем совершать подстановку:
(a,b)->(b,a+b)
Рекурсивный алгоритм, реализованный по этой подстановке, будет иметь вид:
function fib (a,b,n: integer): integer;
begin
if n = 1 then
Result := a
else Result := fib(b,a+b,n-1)
end;
begin
for var i:=1 to 10 do
Print(fib(1,1,i));
end.Рекурсия в данном примере - концевая. Как уже отмечалась, она легко заменяется итерацией, при этом как раз получается предыдущее итерационное решение. Хорошие оптимизирующие компиляторы делают это автоматически.
Пример хорошего использования рекурсии - ханойские башни
Задача состоит в следующем:
Даны три стержня. На первом лежат n дисков разного радиуса при условии, что ни один диск бОльшего радиуса не лежит на диске мЕньшего радиуса.
Hеобходимо перенести диски с первого стержня на третий, пользуясь вторым, при условии:
- за один ход можно переносить только один диск
- меньший диск должен лежать на большем
Идея алгоритма такая:
перекладываем n-1 диск с исходного стержня на вспомогательный оставшийся диск перекладываем на требуемый стержень лежащие на вспомогательном стержне диски перекладываем на требуемый диск
Т.о. имеем простое рекурсивное решение:
procedure MovePiramid(n: integer; f, t, w : integer);
begin
if n = 0 then
exit;
MovePiramid(n - 1, f, w, t);
writelnFormat('Переложить диск с {0} на {1}', f, t);
MovePiramid(n - 1, w, t, f);
end;Быстрая сортировка
<xh4>Алгоритм</xh4>
Алгоритм быстрой сортировки (разновидность алгоритма «разделяй и влавствуй») состоит из двух этапов:
1. Выбор некоторого элемента массива x и разделение массива на две части так, что в первой оказываются все элементы <= x, а в о второй — >= x
2. Рекурсивное применение нашего алгоритма к полученным частям
Очевидно, алгоритм будет работать тем быстрее, чем на более равные части мы будем делить массив (в идеале — каждый раз пополам).
Поэтому мы должны стремиться выбрать элемент x так, чтобы примерно половина элементов массива была <= его, и, соответственно, вторая половина — >=. С другой стороны, выбор x не должен занимать много времени и, по крайней мере, не зависеть от n — размера массива).
Мы будем использовать простейший способ выбора x — в качестве него брать первый элемент.
На следующей анимации представлен пример применения алгоритма быстрой сортировки к массиву
4 1 7 3 2 9 5 8 6
Рассмотрим этап 1 подробнее:
- Для разделения массива на указанные части заведем 2 индекса i и j.
- В начале i будет указывать на первый элемент и двигаться вправо, а j — на последний и двигаться влево.
Шаг 1.
Будем продвигать i вперед до тех пор, пока A[i] не станет >= x.
Далее будем продвигать j назад до тех пор, пока A[j] не станет <= x.
Пришли к элементам A[i] и A[j], которые "стоят не на своих местах" (вспомним, что мы хотим раскидать все меньшие или равные x элементы влево, а большие или равные — вправо)
Шаг 2.
Поменяем их местами и продвинем i вперед на один элемент, а j — назад, также на один элемент.
Будем повторять указанные действия до тех пор, пока i не станет >= j.
В результате получим массив A, разделенный на 2 части:
- слева все элементы <= x
- справа — >= x
Код программы
// Быстрая сортировка Ч. Хоара
/// Разделение a[l]..a[r] на части a[l]..a[q] <= a[q+1]..a[r]
function Partition(a: array of integer; l,r: integer): integer;
begin
var i := l - 1;
var j := r + 1;
var x := a[l];
while True do
begin
repeat
Inc(i);
until a[i]>=x;
repeat
Dec(j);
until a[j]<=x;
if i<j then
Swap(a[i],a[j])
else
begin
Result := j;
exit;
end;
end;
end;
/// Сортировка частей
procedure QuickSort(a: array of integer; l,r: integer);
begin
if l>=r then exit;
var j := Partition(a,l,r);
QuickSort(a,l,j);
QuickSort(a,j+1,r);
end;
const n = 20;
begin
var a := ArrRandom();
writeln('До сортировки: ');
Writeln(a);
QuickSort(a,0,a.Length-1);
writeln('После сортировки: ');
Writeln(a);
end.<xh4>Асимптотическая оценка сложности</xh4>
Будем исходить из того, что массив всякий раз делится на 2 одинаковые части. Это самый лучший вариант.
Глубина рекурсии в этом случае = log2n.
Очевидно, что в алгоритме Partition мы просматриваем все элементы «своей части» ровно один раз. Т.е. на каждом уровне рекурсии будут по одному разу просмотрены все элементы массива.
Это означает, что асимптотическая сложность Partition на каждом уровне рекурсии = Θ(n).
Т.о., при условии деления примерно пополам, асимптотическая сложность всего алгоритма = Θ(n log n).
Теоретически доказано, что в среднем, если делим не точно пополам, асимптотическая сложность сохраняет формулу Θ(n log n).
Вопрос: какова сложность в худшем случае? Худший — когда в качестве x выбираем минимальный (или максимальный) элемент. Это происходит (в нашей ситуации, т.к. мы выбираем первый элемент), если массив уже отсортирован.
В этом случае в результате разбиения на части большая часть будет уменьшаться на 1, и глубина рекурсии в процедуре Sort будет равна <math>n - 1</math>.
Поэтому в худшем случае асимптотическая сложность = <math>\Theta(n^2)</math>.
Утверждение. Для произвольных данных не существует алгоритма с асимптотической сложностью лучше, чем Θ(n log n) в среднем.
Генерация всех перестановок
Основная идея алгоритма генерации всех перестановок заключается в следующем. В массиве длины n, содержащем перестановку, будем менять последний элемент с каждым, после чего будем рекурсивно будем делать то же самое для массива длины n-1 и затем возвращать переставленный элемент на старое место. Если достигнута длина массива n=1, то переставлять ничего не нужно, а следует выдавать содержимое всего массива-перестановки на экран. Такой алгоритм позволит сгенерировать все перестановки, что следует из словесного рекурсивного определения: на последнем месте побывает каждый элемент, содержащийся в рассматриваемом массиве, после чего к оставшейся части массива рекурсивно будет применен тот же алгоритм.
procedure Perm(a: array of integer; n: integer);
begin
if n=1 then
Writeln(a)
else
for var i:=0 to n-1 do
begin
Swap(a[i],a[n-1]);
Perm(a,n-1);
Swap(a[i],a[n-1]);
end;
end;
const n=3;
begin
var a := ArrGen(n,i->i,1);
Perm(a,n);
end.Нетрудно видеть, что глубина рекурсии составляет n-1, а количество вызовов процедуры Perm составляет n!.
Генерация всех подмножеств
Генерация всех подмножеств представляет собой алгоритм перебора. В алгоритмах перебора перебираются все варианты и для подходящих вариантов выполняется определенное действие. В данном случае просто выводятся все подмножества.
procedure Generate(A: array of integer; i: integer; Subset: LinkedList<integer>);
begin
if i = A.Length then
Subset.Println
else
begin
Generate(A,i+1,Subset); // не добавлять
Subset.AddLast(A[i]);
Generate(A,i+1,Subset); // добавить
Subset.RemoveLast;
end;
end;
begin
var A := Arr(5,3,8,13,15);
var Subset := new LinkedList<integer>;
Generate(A,0,Subset);
end.Перебор с возвратом (backtracking)
Общая схема перебора с возвратом
procedure backtracking(k: integer); // k - номер хода
begin
{ запись варианта }
if { решение найдено } then
{ вывод решения }
else
{ перебор всех вариантов }
if { вариант подходит } then
backtracking(k+1);
{ стирание варианта }
end;
begin
backtracking(1);
end.Задача об обходе конем шахматной доски
const n = 8;
var
dx := Arr(2, 2, 1, 1, -1, -1, -2, -2);
dy := Arr(1, -1, 2, -2, 2, -2, 1, -1);
type KnightProblem = class
Solution := new integer[n, n];
Success: boolean := false;
procedure Step(i, x, y: integer);
begin
if Success then
exit;
// отсечение неверных вариантов
if (x < 0) or (x >= n) or (y < 0) or (y >= n) or (Solution[x, y] > 0) then
exit;
// запись частичного решения
Solution[x, y] := i;
if i = n * n then
Success := true
else
for var k:=0 to 7 do // перебор вариантов
Step(i + 1, x + dx[k], y + dy[k]);
if not Success then
Solution[x, y] := 0; // возврат - стирание частичного решения
end;
end;
const
x0 = 1; // начальная клетка коня
y0 = 3;
begin
var kp := new KnightProblem();
kp.Step(1, x0, y0);
if kp.Success then
writeln(kp.Solution);
writelnFormat('Время: {0} мс', Milliseconds/1000);
end.Деревья
Деревом назовем совокупность узлов, называемых вершинами дерева, соединенных между собой ребрами, называемыми ветвями.
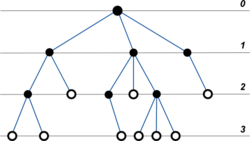
Количество уровней называется глубиной дерева.
Каждая вершина нижнего уровня соединяется ровно с одной вершиной предыдущего уровня.
Единственная вершина на уровне 0 называется корнем дерева.
Она не имеет вершин-предков.
Вершины, не имеющие потомков, называют листьями дерева, а совокупность всех листьев образует крону дерева.
Примеры.
- Дерево папок на диске
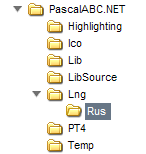
- Самый очевидный пример — генеалогическое древо
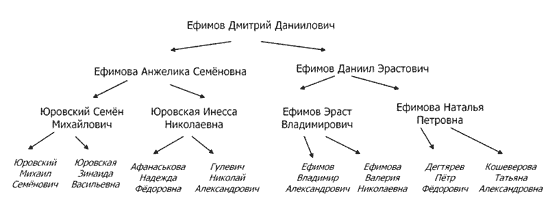
- Главы и пункты книги

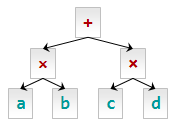
- Дерево разбора выражений
a*b + c*d
Теперь дадим рекурсивное определение дерева:
Дерево ::= корень список_поддеревьев
| ε
Список поддеревьев ::= список_поддеревьев дерево
| ε
// ε означает «пусто»
Определения
Дерево называется бинарным (двоичным), если каждая его вершина имеет не более двух потомков.
(Далее бинарные деревья будем сокращать как БД)
Двоичное_дерево ::= корень левое_поддерево правое_поддерево
| ε
Левое_поддерево ::= двоичное_дерево
Правое_поддерево ::= двоичное_дерево
БД называется идеально сбалансированным, если для каждого узла количество узлов в его правом поддереве отличается от количества узлов в его левом поддереве максимум на единицу. <здесь будут рисунки деревьев>
Полным называют БД, у которого каждая вершина, не являющаяся листом, имеет ровно двух потомков, и все листья находятся на последнем уровне.
Количество узлов (u) и количество ребер (v) в произвольном дереве связаны простой формулой: <math>u = v + 1</math>.
Количество узлов в полном БД вычисляется по формуле
<math>\ 2^{n+1} - 1,</math>
где n — глубина дерева.
Действительно:
u0 = 1 = 20
u1 = 2 = 21
u2 = 4 = 22
...
un = 2n
Значит общее количество узлов в дереве глубины n:
u(n) = 20 + 21 + 22 + ... + 2n
Узнаем геометрическую прогрессию с n + 1 членами. А её сумма:
<math>\ S_{n+1} = b_1 \frac{q^{n+1} - 1}{q - 1} = 1 \frac{2^{n+1} - 1}{2 - 1} = 2^{n + 1} - 1</math>
Порядки обхода деревьев
Требуется составить алгоритм, обходящий все узлы дерева в некотором порядке.
Существует несколько вариантов обходов, каждый из которых описывается рекурсивным алгоритмом.
Рассмотрим эти алгоритмы для обычного и бинарного деревьев:
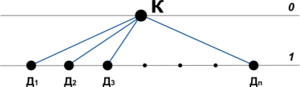
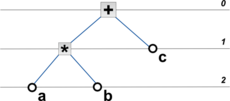
- Инфиксный
- Д1 К Д2 Д3 Дn
- и
- БД: Левое_поддерево Корень Правое_поддерево
- Префиксный
- К Д1 Д2 Д3 ... Дn
- и
- БД: Корень Левое_поддерево Правое_поддерево
- + * a b c — префиксная запись выражения
- Примечание. Для вычисления выражений, записанных в префиксной форме, применяется рекурсивный алгоритм.
- Постфиксный
- Д1 Д2 Д3 ... Дn К
- и
- БД: Левое_поддерево Правое_поддерево Корень
- a b * с + — обратная польская бесскобочная запись выражения
- Или Обратная польская нотация (ОПН) (Обратная бесскобочная запись (ОБЗ), Постфиксная нотация, Бесскобочная символика Лукашевича, Польская инверсная запись, Полиз) —
форма записи математических выражений, в которой операнды расположены перед знаками операций.
Обратная польская нотация была разработана австралийским философом и специалистом в области теории вычислительных машин Чарльзом Хэмблином в середине 1950-х на основе польской нотации, которая была предложена в 1920 году польским математиком Яном Лукасевичем. Работа Хэмблина была представлена на конференции в июне 1957, и издана в 1957 и 1962.
ОПН является наиболее удобной формой записи математических выражений и широко используется в вычислительной технике.
Основными её преимуществами являются возможность однократного просмотра при вычислении и простота преобразования из инфиксной записи (на основе простого алгоритма, предложенного Дейкстрой).
Подробнее см. Википедию
Реализация бинарного дерева
type
TreeNode<T> = class
data: T;
left, right: TreeNode<T>;
constructor (d: T; l, r: TreeNode<T>);
begin
data := d;
left := l;
right := r;
end;
end;<xh4>Создание идеально-сбалансированного бинарного дерева</xh4>
function CreateTree(n: integer): TreeNode<integer>;
begin
if n <= 0 then
Result := nil
else
Result := new TreeNode<integer>(
Random(100),
CreateTree((n-1) div 2),
CreateTree(n - 1 - (n-1) div 2));
end;<xh4> Обходы БД </xh4>
- Инфиксный
procedure InfixPrintTree(root: TreeNode<integer>);
begin
if root = nil then
exit;
InfixPrintTree(root.left);
write(root.data, ' ');
InfixPrintTree(root.right);
end;Заметим, что кроме вывода root.data, над ним можно совершать еще массу действий (например, уменьшать на 1, или выводить его квадрат).
Поэтому есть смысл передавать в процедуру обхода выполняемое действие. Для этого определим процедурный тип и внесем в процедуру соответствующие изменения:
type
IntAction = procedure (var data: integer);
procedure InfixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
if root = nil then
exit;
InfixTraverseTree(root.left, Action);
Action(root.data);
InfixTraverseTree(root.right, Action);
end;- Префиксный
procedure PrefixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
if root = nil then
exit;
Action(root.data);
PrefixTraverseTree(root.left, Action);
PrefixTraverseTree(root.right, Action);
end;- Постфиксный
procedure PostfixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
if root = nil then
exit;
PostfixTraverseTree(root.left, Action);
PostfixTraverseTree(root.right, Action);
Action(root.data);
end;Замечание. Видим, что процедуры отличаются только моментом вызова Action. Поэтому можем избежать дублирования кода, написав процедуру, которой в качестве параметра также передается порядок обхода:
type
/// Порядок обхода
TraversalOrder = (Infix, Prefix, Postfix);
procedure TraverseTree(root: TreeNode<integer>; Action: IntAction; order: TraversalOrder := Infix);
begin
if root = nil then
exit;
if order = Prefix then // если префиксный порядок обхода,
Action(root.data); // то сначала обрабатываем корень
TraverseTree(root.left, Action, order);
if order = Infix then // если инфиксный, то корень надо обработать
Action(root.data); // после левого поддерева, но перед правым
TraverseTree(root.right, Action, order);
if order = Postfix then // и если порядок постфиксный,
Action(root.data); // то корень обрабатывается последним
end;<xh4> Связь деревьев и рекурсии </xh4>
Пусть у нас есть такое бинарное дерево:
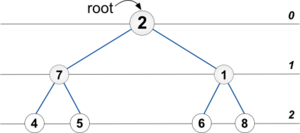
Вызовем процедуру InfixPrintTree(root).
Заметим, что её дерево рекурсивных вызовов совпадет с нашим деревом:
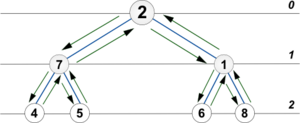
С ним же совпадет и дерево рекурсивных вызовов каждой из процедур: InfixPrintTree, PrefixPrintTree или PostfixPrintTree.
Сделаем несколько замечаний:
- Форма дерева рекурсивных вызовов не зависит от порядка обхода.
- В каждый момент времени глубина рекурсии совпадает с текущей глубиной дерева.
- Стрелочки вниз соответствуют рекурсивному спуску, а стрелочки вверх — рекурсивному возврату.
- Все алгоритмы на деревьях наиболее компактно записываются в рекурсивной форме.
// В ширину
function TraverseTreeWidth<T>(root: Node<T>): sequence of T;
begin
if root = nil then
exit;
var q := new Queue<Node<T>>;
q.Enqueue(root);
while q.Count>0 do
begin
var d := q.Dequeue();
yield d.data;
if d.left<>nil then
q.Enqueue(d.left);
if d.right<>nil then
q.Enqueue(d.right);
end;
end;
// В глубину (нерекурсивный аналог Prefix)
function TraverseTreeDepth<T>(root: Node<T>): sequence of T;
begin
if root = nil then
exit;
var s := new Stack<Node<T>>;
s.Push(root);
while s.Count>0 do
begin
var d := s.Pop();
yield d.data;
if d.right<>nil then
s.Push(d.right);
if d.left<>nil then
s.Push(d.left);
end;
end;
Лекция 9
Задачи на бинарные деревья
Поиск элемента в бинарном дереве
function Find(root: TreeNode<integer>; k: integer): TreeNode<integer>;
begin
if root = nil then
begin
Result := nil;
exit;
end;
if root.data = k then // если нашли элемент, то возвращаем его и прекращаем поиск
begin
Result := root;
exit;
end;
// ищем элемент в левом поддереве
Result := Find(root.left, k);
// если не нашли в левом поддереве, то ищем в правом
if Result = nil then
Result := Find(root.right, k);
end;Примечание. Если в списке находятся несколько искомых элементов, то будет возвращена ссылка на первый из них, а именно — находящийся в «самом левом» поддереве.
Определение минимальной суммы от корня к листу
Решение 1. Очевидный рекурсивный алгоритм
function SimplePathSum(root: TreeNode<integer>): integer;
begin
if root = nil then
Result := integer.MaxValue
else if (root.Left = nil) and (root.Right = nil) then // правка
result := root.Data
else
result := root.Data + Min(SimplePathSum(root.Left), SimplePathSum(root.Right));
end;Здесь осуществляется полный обход дерева (посещение всех узлов)
Решение 2. Алгоритм перебора с возвратом.
Изменим стратегию нахождения минимальной суммы. Будем накапливать сумму в глобальной переменной sum и всякий раз по достижении листа сравнивать ее с глобальной переменной min.
Заметим, что всякий раз мы, добавляя к сумме очередное значение, осуществляем перебор, и если решение неполное, то продолжаем рекурсивные вызовы. После рекурсивных вызовов мы осуществляем возврат суммы к предыдущему значению. В результате в каждой точке в переменной sum хранится сумма элементов от корня к текущему узлу.
Подобный алгоритм называется алгоритмом перебора с возвратами.
var
sum: integer := 0;
min: integer := MaxInt;
procedure MinSumPath1(r: TreeNode<integer>);
begin
if r=nil then
exit;
sum += r.data;
if (r.left=nil) and (r.right=nil) and (sum<min) then
min := sum;
MinSumPath1(r.left);
MinSumPath1(r.right);
sum -= r.data;
end;Данный метод работает примерно с той же скоростью, что и предыдущий (т.к. осуществляется полный перебор). Однако, в отличие от предыдущего метода, он может быть существенно ускорен за счет отсечения заведомо неоптимальных решений. В данном случае если значение sum превысит min, то далее рекурсивные вызовы можно не делать - решение не оптимально (минимум на этом пути достигнут не будет).
Реализуем предыдущий алгоритм в виде функции и уберем все глобальные переменные
function MinSumPath2(r: TreeNode<integer>; sum,min: integer): integer;
begin
if r<>nil then
begin
sum += r.data;
if (r.left=nil) and (r.right=nil) and (sum<min) then
min := sum;
min := MinSumPath2(r.left,sum,min);
min := MinSumPath2(r.right,sum,min);
end;
Result := min;
end;Изменим данный алгоритм, осуществляя выход из рекурсии если сумма на каком-то шаге окажется не меньше min.
Решение 2. Алгоритм перебора с возвратом. Метод ветвей и границ
Метод ветвей и границ является вариацией полного перебора, но производит отсев подмножеств допустимых решений, заведомо не содержащих оптимальных решений.
function MinSumPath3(r: TreeNode<integer>;sum,min: integer): integer;
begin
if r<>nil then
begin
sum += r.data;
if (r.left=nil) and (r.right=nil) and (sum<min) then
min := sum;
if sum<min then
begin
min := MinSumPath3(r.left,sum,min);
min := MinSumPath3(r.right,sum,min);
end;
end;
Result := min;
end;Данный алгоритм работает практически мгновенно.
Вот время работы при n=20000000
- Построение дерева: 6.5 с.
- Алгоритм перебора с возвратом: 0.828 с.
- Метод ветвей и границ: 0.015 с.
Количество рекурсивных вызовов при различных запусках: 25000, 16000, 28000 (в алгоритме 1 количество рекурсивных вызовов равно n=20000000)
Бинарные деревья поиска
- Бинарное дерево называют бинарным деревом поиска (БДП), если для каждого узла дерева выполнено следующее:
все элементы, находящиеся в левом поддереве, меньше элемента в корне, а все элементы, находящиеся в правом поддереве — больше.
Замечание. При такой формулировке определения, БДП не имеет повторяющихся элементов и называется бинарным деревом поиска без повторяющихся элементов.
А если в определении заменить все строгие неравенства на нестрогие, то БДП будет называться бинарным деревом поиска с повторяющимися элементами.
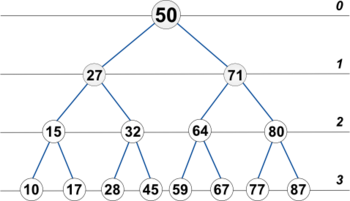
Обойдем наше БДП с помощью инфиксного обхода:
10 15 17 27 28 32 45 50 59 64 67 71 77 80 89
Значит, при инфиксном обходе БДП получаем отсортированную последовательность данных.
Т.о., в каждый момент времени БДП хранит отсортированные данные.
Каково же количество действий при обходе БДП?
Поскольку при обходе мы проходим по каждому ребру дважды (один раз — вниз, на рекурсивном спуске, и один раз — вверх, на рекурсивном возврате), то мы тратим количество действий, в два раза превышающее количество ребер.
Т.к. количество ребер на 1 меньше количества вершин, то всего тратится <math>2(n - 1)</math> действий, где <math>n</math> — количество вершин (для сравнения: в массиве обход занимает <math>n</math> действий.
<xh4>Алгоритм добавления элемента к БДП</xh4>
Алгоритм добавления элемента к БДП с повторяющимися элементами будет немного отличаться от алгоритма добавления к БДП без повторяющихся элементов — во втором случае, если элемент, который мы хотим добавить, в дереве уже есть, мы ничего не делаем.
Этот случай и рассмотрим:
procedure Add(var root: TreeNode<integer>; x: integer);
begin
if root = nil then
begin
root := new TreeNode<integer>(x, nil, nil);
exit;
end;
if x < root.data then
Add(root.left, x)
else if x > root.data then
Add(root.right, x);
end;Теперь создание дерева не представляет сложности:
var n := 15;
var r: TreeNode<integer> := nil;
for var i := 1 to n do // создание случайного БДП с количеством вершин, равным n
Add(r, Random(100));Вспомним, что при инфиксном выводе БДП получаем отсортированную последовательность данных, значит при n вызовах процедуры добавления элемента к БДП, получим отсортированную последовательность из n элементов.
Поэтому данный алгоритм называется алгоритмом сортировки деревом.
Разберемся, сколько действий потребует одно добавление в среднем.
Пусть дерево, в которое мы добавляем, является идеально-сбалансированным, тогда количество его уровней <math>k \approx \; log_2 n</math>, где <math>n</math> — количество узлов.
Видим, что количество операций в Add совпадает глубиной дерева <math>k</math> (при каждом рекурсивном вызове Add мы опускаемся вниз по дереву на 1 уровень, и вставка осуществляется в лист дерева)
Т.о., при добавлении <math>n</math> элементов, в случае, если дерево всякий раз остается близким к идеально-сбалансированному, тратится <math>n\log_2 n</math> действий (столько же, сколько при быстрой сортировке).
Замечание 1. Данная оценка справедлива в среднем.
Замечание 2. Данная оценка совпадает с оценкой количества операций при быстрой сортировке, а значит является оптимальной для произвольных данных.
<xh4>Оценка количества операций при сортировке деревом в худшем случае</xh4> Будем добавлять элементы в БДП в возрастающем порядке:
Add(10); Add(15); Add(17); ... Add(87);
Получим "однобокое" дерево:
10
\
15
\
17
\
...
\
87
При таком порядке добавлений, количество операций составляет примерно <math>n^2</math> (как и в худшем случае быстрой сортировки).
Замечание. Чтобы сохранить асимптотическую оценку <math>n\log_2 n</math> и в худшем случае, всякий раз, при добавлении в дерево, надо проводить так называемую перебалансировку, которая сохраняет свойство дерева быть деревом поиска, но уменьшает, по возможности, его глубину до минимальной.
<xh4>Поиск элемента в БДП</xh4>
function Find(root: TreeNode<integer>; x: integer): boolean;
begin
if root = nil then
Result := false
else if root.data = x then
Result := True
else if x < root.data then
Result := Find(root.left, x)
else // if x > root.data then
Result := Find(root.right, x);
end;Очевидно, количество операций совпадает с глубиной БДП <math>k \approx \; log_2 n</math> в среднем.
Заметим, что алгоритм бинарного поиска в отсортированном массиве занимает столько же действий.
АТД — Абстрактные Типы Данных. Классы как реализация АТД
Что мы знаем о классах
- Класс — это составной тип данных
- Класс, как и запись, содержит поля и методы
- Переменная типа класс и переменная типа запись по-разному хранятся в памяти (ссылочная и размерная организация данных)
- Для создания объекта класса и связывания его с переменной класса вызывается специальная функция-метод, называемая конструктором
- Можно создавать шаблоны классов, параметризованные одним или несколькими типами
Понятие абстрактного типа данных
До сих пор мы сталкивались с конкретными типами данных, которые характеризуются:
- набором допустимых значений
- представлением в памяти
- набором допустимых операций, которые можно выполнять над объектами данного типа
Абстрактный тип данных — это тип данных, доступ к которым осуществляется только через некоторый набор действий (операций, команд).
Этот набор действий называется интерфейсом абстрактного типа данных.
То, как реализован абстрактный тип данных, самим АТД не определяется.
Итак, абстрактный тип данных - это интерфейс, набор операций без реализации.
Класс является одной из возможных реализацией абстрактного типа данных (АТД).
Т.е. класс определяет интерфейс абстрактного типа данных и дает реализацию этого интерфейса (без которой использование АТД невозможно).
Деление операций, расположенных в классе, на интерфейс и реализацию очень важно в современном программировании и называется принципом отделения интерфейса от реализации.
Он заключается в том, что клиентская программа, пользующаяся классом, использует только его интерфейс (в то время, как его реализация важна только разработчикам класса).
Более того, реализацию в классе принято скрывать от клиента специальными конструкциями.
Этот принцип называется принципом сокрытия реализации (или защитой доступа).
А теперь рассмотрим пример абстрактного типа данных — стек.
АТД Стек
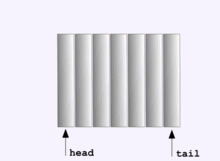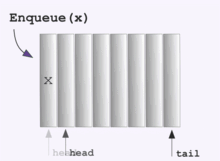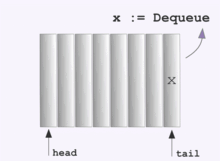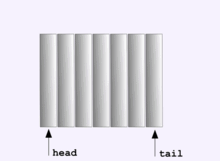
- Стек — это набор данных, устроенный по принципу LIFO (Last In First Out) — последним пришел — первым вышел.
Мы уже знакомы со стеком. Хорошими примерами могут служить программный стек, колода карт или магазин автомата.
Т.о. стек следует представлять как стопку объектов, положенных один на другой. В каждый момент можно:
- положить значение на вершину стека (Push, втолкнуть значение в стек)
- посмотреть значение на вершине стека (Top)
- снять значение с вершины стека (Pop)
- проверить, пуст ли стек (IsEmpty)
Причем, если предмет последним положили на вершину стопки, то он будет снят первым - отсюда и название LIFO.

Описывать стек будем в виде класса.
<xh4>Интерфейс класса Stack</xh4>
type
/// Шаблон класса Stack
Stack<T> = class
constructor Create;
/// Кладет элемент x на вершину стека
procedure Push(x: T);
/// Возвращает элемент типа T, снимая его с вершины стека
function Pop: T;
/// Возвращает значение элемента на вершине стека
function Top: T;
/// Возвращает истину, если стек пуст
function IsEmpty: boolean;
end;Чтобы обеспечить защиту доступа к коду класса, следует поместить описание класса в модуль и откомпилировать его, или же создать библиотеку.
При создании модуля интерфейс класса помещается в интерфейсную секцию модуля, а реализация методов класса — в секцию реализации модуля.
Теперь, когда у нас есть интерфейс класса Stack , напишем клиентскую программу.
Задача. Вычислить выражение, записанное в обратной польской записи (ПОЛИЗ).
- Пусть в строке a хранится выражение в обратной польской бесскобочной нотации, например:
a = '598+46**7+*'
Условимся, что каждый символ представляет собой либо цифру, являющуюся числом, либо знак, являющийся операцией.
<xh4> Алгоритм вычисления выражения в ПОЛИЗ </xh4>
Цикл по символам {
если текущий символ — цифра, то
положить её на стек
иначе, если текущий символ — знак операции, то {
снять со стека два последних числа
совершить над ними указанную операцию
поместить результат на стек
}
}
В результате работы этого алгоритма на стеке останется единственное число, являющееся значением выражения.
Для указанной строчки алгоритм выполнит со стеком следующие операции:
ε (пусто)
5
5 9
5 9 8
5 9 8
+
5 17
5 17 4
5 17 4 6
5 17 4 6
*
5 17 24
5 17 24
*
5 408
5 408 7
5 408 7
+
5 415
5 415
*
2075
Запрограммируем этот алгоритм.
Пусть класс Stack определен в модуле Collections.
Код клиентской программы:
uses Collections;
var
a: string := '598+46**7+*';
s: Stack<real> := new Stack<real>;
begin
for var i := 1 to a.Length do
case a[i] of
'0'..'9': s.Push(StrToInt(a[i]));
'+': s.Push(s.Pop + s.Pop);
'*': s.Push(s.Pop * s.Pop);
'-': begin
var minuend := s.Pop;
var subtrahend := s.Pop;
s.Push(minuend - subtrahend);
end;
'/': begin
var dividend := s.Pop;
var divisor := s.Pop;
s.Push(dividend / divisor);
end;
end;
writeln(s.Pop);
Assert(s.IsEmpty);
end.Замечание 1. Именно деление на интерфейс и реализацию позволило нам приступить к написанию клиентской программы, имея только интерфейс класса Stack и ничего не зная о его реализации.
Т.о. в большом проекте налицо разделение обязанностей:
- Одна группа программистов — разработчики библиотек — создают АТД в виде классов и предоставляют остальным интерфейс этих классов
- Другая группа программистов пользуется этими классами, как АТД, вызывая методы интерфейсов этих классов
При таком способе разделения обязанностей обычно используется следующий сценарий:
- Вначале быстро создается первая реализация класса (неэффективная) и предоставляется клиентам
- Клиенты с помощью этой реализации пишут клиентские программы
- В этот момент группа разработчиков класса делает более эффективную реализацию, после чего меняет на неё исходную.
При этом, все уже написанные клиентские программы продолжают работать.
Замечание 2. Поскольку интерфейс впоследствии поменять практически нельзя (в отличие от реализации), разработка интерфейсов является важнейшим мероприятием на начальном этапе разработки проекта.
<xh4> Реализация стека на базе массива </xh4>
unit Collections;
interface
type
/// Шаблон класса Stack
Stack<T> = class
private // содержимое этой секции недоступно из клиентской программы
/// Массив элементов стека
datas: array of T;
/// Индекс первого пустого элемента
tp: integer;
public // содержимое этой секции открыто для клиентской программы
constructor Create;
/// Кладет элемент x на вершину стека
procedure Push(x: T);
/// Возвращает элемент типа T, снимая его с вершины стека
function Pop: T;
/// Возвращает значение элемента на вершине стека
function Top: T;
/// Возвращает истину, если стек пуст
function IsEmpty: boolean;
end;
implementation
/// Максимальный размер стека
const MAX_STACK = 1000;
constructor Stack<T>.Create;
begin
tp := 0;
SetLength(datas, MAX_STACK);
end;
{Кладет элемент x на вершину стека}
procedure Stack<T>.Push(x: T);
begin
Assert(tp < MAX_STACK);
datas[tp] := x;
tp += 1;
end;
{Возвращает элемент типа T, снимая его с вершины стека}
function Stack<T>.Pop: T;
begin
Assert(not IsEmpty);
result := datas[tp-1];
tp -= 1;
end;
{Возвращает значение элемента на вершине стека}
function Stack<T>.Top: T;
begin
Assert(not IsEmpty);
result := datas[tp-1];
end;
{Возвращает истину, если стек пуст}
function Stack<T>.IsEmpty: boolean;
begin
result := (tp <= 0);
end;
end.<xh4> Реализация стека на базе односвязного линейного списка </xh4>
unit Nodes;
interface
type
/// Узел с одним полем связи
SingleNode<DataType> = class
/// Значение
data: DataType;
/// Ссылка на следующий элемент
next: SingleNode<DataType>;
constructor (dt: DataType; nxt: SingleNode<DataType>);
begin
data := dt;
next := nxt;
end;
end;
implementation
end.unit Collections;
interface
uses Nodes;
type
/// Шаблон класса Stack
Stack<T> = class
private // содержимое этой секции недоступно из клиентской программы
/// Указатель на вершину стека
tp: SingleNode<T> := nil;
public // содержимое этой секции открыто для клиентской программы
constructor Create;
/// Кладет элемент x на вершину стека
procedure Push(x: T);
/// Возвращает элемент типа T, снимая его с вершины стека
function Pop: T;
/// Возвращает значение элемента на вершине стека
function Top: T;
/// Возвращает истину, если стек пуст
function IsEmpty: boolean;
end;
implementation
constructor Stack<T>.Create;
begin
tp := nil;
end;
{Кладет элемент x на вершину стека}
procedure Stack<T>.Push(x: T);
begin
tp := new SingleNode<T>(x, tp);
end;
{Возвращает элемент типа T, снимая его с вершины стека}
function Stack<T>.Pop: T;
begin
Assert(not IsEmpty);
result := tp.data;
tp := tp.next;
end;
{Возвращает значение элемента на вершине стека}
function Stack<T>.Top: T;
begin
Assert(not IsEmpty);
result := tp.data;
end;
{Возвращает истину, если стек пуст}
function Stack<T>.IsEmpty: boolean;
begin
result := (tp = nil);
end;
end.АТД и класс Очередь
- Очередь — это набор данных, устроенный по принципу FIFO (First In First Out) — первым пришел — первым вышел.
В каждый момент можно:
- добавить значение в хвост очереди (Enqueue)
- убрать значение из головы очереди (Dequeue)
- проверить, пуста ли очередь (IsEmpty)
Оформим АТД «очередь» в виде шаблона класса.
<xh4> Интерфейс класса Queue </xh4>
type
/// Шаблон класса Queue
Queue<T> = class
constructor Create;
/// Добавляет элемент x в хвост очереди
procedure Enqueue(x: T);
/// Возвращает элемент типа T, убирая его из головы очереди
function Dequeue: T;
/// Возвращает истину, если очередь пуста
function IsEmpty: boolean;
end;<xh4> Реализация очереди на базе односвязного линейного списка </xh4>
unit Collections;
interface
uses Nodes;
type
// Здесь описан шаблон класса Stack
/// Шаблон класса Queue
Queue<T> = class
private
/// Голова очереди
head: SingleNode<T>;
/// Хвост очереди
tail: SingleNode<T>;
public
constructor Create;
/// Добавляет элемент x в хвост очереди
procedure Enqueue(x: T);
/// Возвращает элемент типа T, убирая его из головы очереди
function Dequeue: T;
/// Возвращает истину, если очередь пуста
function IsEmpty: boolean;
end;
implementation
// Здесь реализованы методы шаблона класса Stack
constructor Queue<T>.Create;
begin
head := nil;
tail := nil;
end;
{Добавляет элемент x в хвост очереди}
procedure Queue<T>.Enqueue(x: T);
begin
if IsEmpty then
begin
head := new SingleNode<T>(x, nil);
tail := head;
end
else // if not IsEmpty
begin
tail.next := new SingleNode<T>(x, nil);
tail := tail.next;
end;
end;
{Возвращает элемент типа T, убирая его из головы очереди}
function Queue<T>.Dequeue: T;
begin
Assert(not IsEmpty);
result := head.data;
head := head.next;
if head = nil then
tail := nil;
end;
{Возвращает истину, если очередь пуста}
function Queue<T>.IsEmpty: boolean;
begin
result := (head = nil);
end;
end.Примеры использования АТД Queue
Наследование
Основные определения
Наследование в программировании возникло как ответ на реальные отношения наследования классов в реальном мире и прикладных задачах.
————————————
Ввиду увеличения сложности задач в программировании, акцент переместился от алгоритмов к объектам, содержащим алгоритмы в качестве методов.
При этом, понятие главного алгоритма также потеряло свою важность. В больших проектах нет главного алгоритма или он тривиален, но есть большое число взаимосвязанных задач.
Пример. Главный алгоритм работы операционной системы.
* начальная инициализация
* цикл обработки сообщений
если сообщение пришло то
обработать сообщение
до сообщения «Конец»
* заключительные действия
Как видим, этот алгоритм тривиален и ничего не говорит о том, как работает ОС.
————————————
Поскольку главный алгоритм сложной системы не существует или тривиален, то для программирования работы этой сложной системы мы:
- выявляем классы объектов, присутствующих в этой системе
- их свойства и методы
- выявляем то общее, что есть в различных классах
- выявляем различные зависимости между классами и взаимодействие между объектами этих классов
Примеры зависимостей между классами
- класс содержит в качестве поля объект другого класса
- в методе класса параметром является объект другого класса
- метод класса вызывает статический метод другого класса
- один из классов является разновидностью другого
Определение. Наследованием называется такая зависимость между классами, при которой один из классов является разновидностью другого.
При наследовании все члены базового класса (поля, методы, свойства) переходят в производный (наследуются им). Кроме того, производный класс может добавлять новые члены (поля, методы, свойства) и переопределять (замещать) методы базового класса.
Для классов, связанных наследованием, используют следующие термины:
- базовый — производный
- предок — потомок
- надкласс — подкласс
Каковы цели наследования?
- Повторное использование кода.
- Обеспечение вариабельности и изменчивости кода.
Наследование — это расширение или сужение?
Наследование — это расширение интерфейса класса, но сужение количества объектов (представителей) класса.
Наследование на примере Student - SeniorStudent
Про переменную Self см. здесь.
Рассмотрим следующий пример наследования:
Класс SeniorStudent (студент старших курсов) является разновидностью класса Student. Будем считать, что на младших курсах студент еще не знает, сколько лет он будет учиться и какую академическую степень получит, поэтому считается, что он учится 4 года. Будем также считать, что он узнает, какую академическую степень получит (бакалавр, специалист, магистр), когда становится студентом старших курсов (SeniorStudent). В этот же момент к нему прикрепляется научный руководитель из числа преподавателей (Teacher).
<xh4> Базовый класс Student </xh4>
interface
uses System;
const
/// Минимальный допустимый возраст студента
MIN_AGE = 1;
/// Максимальный допустимый возраст студента
MAX_AGE = 120;
/// Первый курс
FIRST_COURSE = 1;
/// Максимальный курс для студентов младших курсов
LAST_UNDERGRADUATE_COURSE = 4;
type
/// Студент
Student = class
private
fName: string;
fAge, fCourse, fGroup: integer;
public
/// Имя — только на чтение
property Name: string read fName;
/// Возраст — только на чтение
property Age: integer read fAge;
/// Курс — только на чтение
property Course: integer read fCourse;
/// Группа — только на чтение
property Group: integer read fGroup;
/// <summary>
/// Создает нового студента
/// </summary>
/// <param name="Name">Имя (пустое недопустимо)</param>
/// <param name="Age">Возраст (отрицательный или больший MAX_AGE недопустим)</param>
/// <param name="Course">Курс (отрицательный или больший LAST_UNDERGRADUATE_COURSE недопустим)</param>
/// <param name="Group">Группа (отрицательная недопустима)</param>
constructor Create(Name: string; Age, Course, Group: integer);
procedure SetAge(Age: integer);
procedure SetGroup(Group: integer);
/// Переводит студента на следующий курс, если он меньше LAST_UNDERGRADUATE_COURSE
procedure NextCourse;
procedure Print;
procedure Println;
end;
implementation
constructor Student.Create(Name: string; Age, Course, Group: integer);
begin
if Name <> '' then
fName := Name
else
raise new Exception(
'Попытка присвоить студенту пустое имя!');
SetAge(Age);
if (Course >= FIRST_COURSE) and (Course <= LAST_UNDERGRADUATE_COURSE) then
fCourse := Course
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + LAST_UNDERGRADUATE_COURSE.ToString + ']!');
SetGroup(Group);
end;
procedure Student.SetAge(Age: integer);
begin
if (Age >= MIN_AGE) and (Age <= MAX_AGE) then
fAge := Age
else
raise new Exception(
'Выход за границы диапазона допустимого возраста [' +
MIN_AGE.ToString + '..' + MAX_AGE.ToString + ']!');
end;
procedure Student.SetGroup(Group: integer);
begin
if (Group > 0) then
fGroup := Group
else
raise new Exception(
'Попытка присвоить группе отрицательный номер!');
end;
procedure Student.NextCourse;
begin
if fCourse < LAST_UNDERGRADUATE_COURSE then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + LAST_UNDERGRADUATE_COURSE.ToString + ']!');
end;
procedure Student.Print;
begin
WriteFormat(
'Имя: {0} Возраст: {1} Курс: {2} Группа: {3} ',
fName, fAge, fCourse, fGroup);
end;
procedure Student.Println;
begin
Print;
writeln();
end;<xh4> Производный класс SeniorStudent </xh4>
SeniorStudent — студент старших курсов.
Помимо имени, возраста, курса и группы:
- у него будет научный руководитель (Advisor: Teacher)
- он будет знать тему курсовой работы, которую получает от своего научного руководителя
- и для него будет известно, какую он получает академическую степень Degree (бакалавра, специалиста или магистра)
Будем считать, что класс преподавателя у нас уже есть, и у него есть метод SayCourseWorkTheme(MyStudent: SeniorStudent): string.
Приступим к реализации SeniorStudent.
Для начала нам понадобится вспомогательный тип DegreeType (академическая степень):
type
/// Академическая степень (Бакалавр, Специалист, Магистр)
DegreeType = (Bachelor, Specialist, Magister);Теперь напишем интерфейс нашего старшекурсника:
/// Студент старших курсов
SeniorStudent = class (Student)
private
fAdvisor: Teacher;
fDegree: DegreeType;
public
/// Научный руководитель — только на чтение
property Advisor: Teacher read fAdvisor;
/// Образовательная степень — только на чтение
property Degree: DegreeType read fDegree;
/// <summary>
/// Создает нового студента старших курсов
/// </summary>
/// <param name="Name">Имя (пустое недопустимо)</param>
/// <param name="Age">Возраст (отрицательный или больший MAX_AGE недопустим)</param>
/// <param name="Course">Курс (отрицательный или больший MAX_COURSE недопустим)</param>
/// <param name="Group">Группа (отрицательная недопустима)</param>
/// <param name="Advisor">Научный руководитель</param>
/// <param name="EduModel">Академическая степень (бакалавр, специалист, магистр)</param>
constructor Create(Name: string; Age, Course, Group: integer;
Advisor: Teacher; Degree: DegreeType);
/// Возвращает тему курсовой работы
function CourseWorkTheme: string;
procedure NextCourse;
procedure Print;
procedure Println;
end;Как CourseWorkTheme и NextCourse мы знаем:
function SeniorStudent.CourseWorkTheme: string;
begin
Result := fAdvisor.SayCourseWorkTheme(self);
end;
procedure SeniorStudent.NextCourse;
begin
var lastCourse: integer;
case fDegree of
Bachelor: lastCourse:= 4;
Specialist: lastCourse:= 5;
Magister: lastCourse:= 6;
end;
if fCourse < lastCourse then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + lastCourse.ToString + ']!');
end;Замечание. В процессе разработки возникла проблема доступа к приватным полям предка (fCourse)
Если Student и SeniorStudent реализованы в одном модуле, то такой проблемы нет и доступ возможен, однако, если они они реализованы в разных модулях, то данный код не откомпилируется.
Исправим это в дальнейшем, а пока будем считать, что классы реализованы в одном модуле.
Заметим, что процедура NextCourse была полностью переопределена в потомке.
Но, как правило, одноименный метод в потомке не переписывается полностью, а вызывает соответствующий метод предка.
Напомним, что переопределяющий метод называется также замещающим.
Для вызова в методе Method замещенного метода предка используется конструкция
inherited Method
Inherited — значит унаследованный.
Воспользуемся этим при реализации оставшихся методов:
constructor SeniorStudent.Create(Name: string; Age, Course, Group: integer;
Advisor: Teacher; Degree: DegreeType);
begin
inherited Create(Name, Age, Course, Group);
if Advisor <> nil then
fAdvisor := Advisor
else
raise new Exception(
'Параметр «Advisor» конструктора является нулевой ссылкой!');
fDegree := Degree;
end;
procedure SeniorStudent.Print;
begin
inherited Print;
write('Преподаватель: ');
fAdvisor.Print;
write('Академическая степень: ');
case fDegree of
Bachelor: write('Бакалавр');
Specialist: write('Специалист');
Magister: write('Магистр');
end;
end;
procedure SeniorStudent.Println;
begin
Print;
writeln();
end;Полный текст модуля University
Вызов унаследованных конструкторов
- Конструктор — это функция, создающая объект класса и возвращающая ссылку на него.
Вспомним, как выглядел конструктор класса SeniorStudent (студента старших курсов):
type SeniorStudent = class (Student)
...
constructor SeniorStudent.Create(Name: string; Age, Course, Group: integer;
Advisor: Teacher; Degree: DegreeType);
begin
{*} inherited Create(Name, Age, Course, Group);
if Advisor <> nil then
fAdvisor := Advisor
else
raise new Exception(
'Параметр «Advisor» конструктора является нулевой ссылкой!');
fDegree := Degree;
end;
...
var ss: SeniorStudent := new SeniorStudent(...);- (*) Унаследованный конструктор базового класса вызывается как процедура, т.е. возвращаемое значение игнорируется.
Вопрос. Создает ли вызов унаследованного конструктора базового класса объект в динамической памяти?
Ответ. Нет. Объект создается вызовом конструктора производного класса. А вызов унаследованного конструктора производится как вызов обычного метода.
Вопрос. Можно ли совершать вызов унаследованного конструктора не первым оператором в коде основного конструктора?
Ответ. В PascalABC.NET нельзя, как и в таких языках, как Java, C++ и C#.
Принцип «открыт - закрыт»
Принцип «открыт - закрыт» состоит в следующем: код программы должен быть закрыт для изменения текста и открыт для модификации поведения и функциональности.
Чтобы обеспечить этот принцип в современном программировании используют наследование: от базового класса, в котором не хватает функциональности, порождают новый, добавляя и изменяя его функциональность.
Код базового класса при этом не меняется.
Замечание. Базовый класс в настоящем должен проектироваться с учетом будущих изменений. Т.е. так, чтобы в будущем мы могли породить от него потомка с нужной нам функциональностью.
Пример. Очередь с подсчетом элементов.
Реализуем класс очереди с подсчетом элементов (CountingQueue<T>) как производный от обычной очереди (Queue<T>) (см. модуль Collections):
interface
uses Collections;
type
/// Очередь с подсчетом элементов
CountingQueue<T> = class (Queue<T>)
private
/// Количество элементов
fCount: integer;
public
/// Количество элементов
property Count: integer read fCount;
/// Создает пустую очередь
constructor Create;
/// Добавляет элемент x в хвост очереди
procedure Enqueue(x: T);
/// Возвращает значение элемента в голове, удаляя его из очереди
function Dequeue: T;
end;
implementation
constructor CountingQueue<T>.Create;
begin
inherited Create;
fCount := 0;
end;
{Добавляет элемент x в хвост очереди}
procedure CountingQueue<T>.Enqueue(x: T);
begin
inherited Enqueue(x);
fCount += 1;
end;
{Возвращает значение элемента в голове, удаляя его из очереди}
function CountingQueue<T>.Dequeue: T;
begin
Result := inherited Dequeue;
fCount -= 1;
end;
end.Замечание. В классе CountingQueue часть методов унаследована от класса Queue без замещения (например, метод IsEmpty).
Наследование и включение
Реализуем класс CountingQueue другим способом: включим очередь Queue в качестве приватного поля в класс CountingQueue и переопределим все методы очереди, делегируя вызов методов внутреннему объекту класса Queue:
interface
uses Collections;
type
/// Очередь с подсчетом элементов (на базе Queue)
CountingQueue<T> = class
private
/// Встроенная очередь
fq: Queue<T>; // включение объекта класса
/// Количество элементов
fCount: integer;
public
/// Количество элементов
property Count: integer read fCount;
/// Создает пустую очередь
constructor Create;
/// Добавляет элемент x в хвост очереди
procedure Enqueue(x: T);
/// Возвращает значение элемента в голове, удаляя его из очереди
function Dequeue: T;
/// Возвращает значение элемента в голове очереди, не удаляя его
function First: T;
/// Возвращает истину, если очередь пуста
function IsEmpty: boolean;
end;
implementation
constructor CountingQueue<T>.Create;
begin
fq := new Queue<T>;
fCount := 0;
end;
{Добавляет элемент x в хвост очереди}
procedure CountingQueue<T>.Enqueue(x: T);
begin
fq.Enqueue(x);
fCount += 1;
end;
{Возвращает значение элемента в голове, удаляя его из очереди}
function CountingQueue<T>.Dequeue: T;
begin
Result := fq.Dequeue;
fCount -= 1;
end;
{Возвращает значение элемента в голове очереди, не удаляя его}
function CountingQueue<T>.First: T;
begin
Result := fq.First;
end;
{Возвращает истину, если очередь пуста}
function CountingQueue<T>.IsEmpty: boolean;
begin
Result := fq.IsEmpty;
end;
end.В данном случае способ реализации с включением объекта класса хуже способа наследования от этого класса по следующим причинам:
- Мы считаем класс CountingQueue разновидностью класса Queue, поэтому он должен содержать все, что есть в Queue, и, возможно, что-то еще
- При включении нам придется, поэтому, переопределять все методы, а при наследовании — только необходимые
А вот в примере, где мы определяли класс SimpleSet на базе динамического массива, мы пользовались включением.
Почему тогда не использовалось наследование? Зададим вопрос: а является ли множество разновидностью динамического массива? Ответ: нет.
<xh4> Когда выбирать наследование, а когда — включение? </xh4>
Есть два класса: A и B.
Зададим вопросы:
- B является разновидностью A?
(B is A?)
Если ответ «да», то это — наследование. - A состоит из B?
(A has B?)
Если ответ «да», то это — включение. - A использует объект B для реализации?
(A use B?)
Если ответ «да», то это — включение.
Однако, не всегда ответы на эти вопросы однозначны. Приведем несколько примеров.
- Matrix является разновидностью Vector.
Да. Можем рассматривать Matrix как вектор-строку, состоящую из векторов-столбцов. - Vector является разновидностью Matrix.
Тоже да. Можем рассматривать Vector как Matrix из одного столбца. - Matrix состоит из Vector.
Да.
Как видим, эти утверждения противоречивы. Становится понятно, что не всегда можно однозначно определить отношения между классами. Это зависит от задачи.
Приведем еще один пример: Circle и Ellipse.
С точки зрения аналитической геометрии, окружность — это разновидность эллипса. А с точки зрения программирования, возможно, удобнее унаследовать эллипс от окружности (Ведь окружность характеризуется координатами центра и радиусом, а эллипс — координатами центра и двумя радиусами. Поэтому можно реализовать эллипс, добавив к окружности еще один радиус).
Виды отношений между классами (нотация UML-диаграмм классов)
- Ассоциация (связь)

- Агрегация (слабая форма has — состоит логически)

- Композиция (сильная форма has — состоит физически)

- Наследование (обобщение)

- Реализация интерфейсов

(пока не знаем)
Пример 1. UML-диаграмма классов: персона, преподаватель, студент, студент старших курсов, группа.
Пример 2. UML-диаграмма факультета.
Вид доступа protected. Рефакторинг метода NextCourse
Иногда возникает необходимость разрешить доступ к полям или методам предка в методе потомка, но запретить для всех остальных. Такой вид доступа называется protected (защищенный).
Поскольку в одном модуле все имеют доступ и к приватной, и к публичной секциям класса, то данный вид доступа в Pascal'е имеет смысл только, если предок и потомок находятся в разных модулях.
Вернемся к примеру Student <— SeniorStudent: и у обычного студента, и у студента старших курсов есть метод NextCourse
procedure Student.NextCourse;
begin
if fCourse < LAST_UNDERGRADUATE_COURSE then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + LAST_UNDERGRADUATE_COURSE.ToString + ']!');
end;
...
procedure SeniorStudent.NextCourse;
begin
var lastCourse: integer;
case fDegree of
Bachelor: lastCourse := 4;
Specialist: lastCourse := 5;
Magister: lastCourse := 6;
end;
if fCourse < lastCourse then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + lastCourse.ToString + ']!');
end;Проведем рефакторинг (изменение кода с целью улучшения, не влияющее на функциональность) нашего кода, т.к., если классы Student и SeniorStudent находятся в разных модулях, то у SeniorStudent нет доступа к приватному полю fCourse предка Student.
Выход: сделать fCourse protected-полем:
Student = class
private
fName: string;
fAge, fGroup: integer;
protected
fCourse: integer;
public
...
end;Замечание. Делать protected-поля и методы надо только в крайнем случае, т.к. они ослабляют защиту доступа.
Теперь проведем рефакторинг метода NextCourse.
1. Заметим, что реализации этого метода у предка и потомка включают очень похожие части:
(Student)
if fCourse < LAST_UNDERGRADUATE_COURSE then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + LAST_UNDERGRADUATE_COURSE.ToString + ']!');(SeniorStudent)
if fCourse < lastCourse then
fCourse += 1
else
raise new Exception(
'Выход за границы диапазона допустимых курсов [' +
FIRST_COURSE.ToString + '..' + lastCourse.ToString + ']!');Оформим их в специальный метод ProtectedNextCourse(lastCourse) и поместим данный метод в protected-секцию класса Student. Тогда им можно будет пользоваться в методах классов Student, SeniorStudent, и нигде более.
Поскольку упоминание поля fCourse теперь полностью находится в методе ProtectedNextCourse, это поле вновь можно сделать приватным в классе Student.
2. Оформим участок кода метода SeniorStudent.NextCourse:
var lastCourse: integer;
case fDegree of
Bachelor: lastCourse := 4;
Specialist: lastCourse := 5;
Magister: lastCourse := 6;
end;в виде глобальной функции LastCourseByDegree(degree), которая возвращает последний курс, соответствующий академической степени degree.
Полный текст модулей после рефакторинга
Наследование и выявление общего предка
Пример 1.
Рассмотрим следующие классы:
Вынесем то общее, что есть в классах Student и Teacher в базовый класс Person:
Пример 2.
Рассмотрим следующие классы:
Point - x - y + Draw()
Circle - radius + Draw()
Какой класс является предком, а какой потомком?
Пусть потомок — окружность.
Замечание. Данный вид наследования неудачен, т.к. окружность не наследуется от «точки с возможностью рисования», а скорее содержит точку как центр. Но, и окружность, и точка являются разновидностями некоторого класса, содержащего координаты и метод Draw.
Поэтому правильнее сделать так :
Присваивание в иерархии предок-потомок
Рассмотрим уже знакомую иерархию классов:
Что будет происходить при выполнении следующего кода?
begin
var s: Student := new Student('Иванов', 17, 1, 11);
var p: Person := new Person('Петров', 23);
s := p;
p := s;
end;Правило: Переменной базового класса можно присваивать объект производного класса. Это соответствует тому, что ячейка памяти отведённая под переменную базового класса, будет хранить адрес объекта производного класса.
Переменной производного класса нельзя присвоить объект базового класса.
Соответствующий принцип в объектно-ориентированном программировании получил название принципа подстановки: во всех ситуациях, где используется объект базового класса, можно использовать объект производного класса без потери функциональности.
В соответствии со сказанным получаем:
s := p; // ошибка компиляции
p := s; // корректное присваиваниеПример.
Группу студентов послали на субботник. Без потери функциональности можно отправить на субботник:
- студентов младшекурсников
- студетнтов старшекурсников
- аспирантов
Что же происходит при присваивании
p := s;В этом присваивании возникает приведение типа от производного класса к базовому (UpCast).
Приведение же от базового типа к производному (DownCast) осуществляется только с помощью явного приведения типа:
var p: Person;
p := new Student('Иванов', 17, 1, 11);
var s : Student;
s := Student(p); // явное приведение типа
s.NextCourse;Примечание. Для явного приведения типа не обязательно явно создавать переменную, можем воспользоваться уже известной конструкцией
Student(p).NextCourse;Замечание. Если к моменту явного приведения типа в переменной p находится объект базового класса, то возникнет исключение и программа завершится с ошибкой.
var p := new Student('Петров', 23);
var s := Student(p); // ошибка выполненияОперации is и as
<xh4> is </xh4>
p is StudentВозвращает true, если переменная p ссылается в данный момент на объект типа Student (или производного от него типа) и false в противном случае.
Пример.
if p is Student then
Student(p).NextCourse;<xh4> as </xh4>
p as StudentВозвращает ссылку на студента, если преобразование возможно, и nil в противном случае.
Пример.
var s: Student := p as Student;
if s <> nil then
s.NextCourse;Замечание. Код с as будет работать немного быстрее, т.к. в первом примере преобразование, фактически, осуществляется дважды: первый раз — в операции is, а второй — при явном приведении типа.
Исключения
Введение. Что нам уже известно об исключениях
Впервые мы столкнулись с исключениями в начале курса, когда изучали оператор ввода и обработку ошибок ввода с помощью блока try..except.
Позже, при работе с файлами, возник термин «исключение». Мы узнали, как обрабатывать исключения с помощью оператора try..except и познакомились с оператором try..finally.
И, наконец, мы научились генерировать собственные исключения.
Теперь пришло время подробнее изучить исключения.
Иерархия исключений в .NET
Стандартные исключения связаны отношением наследования. Базовым классом для всех исключений является класс Exception, который находится в пространстве имен System.
<xh4> Классы исключений в .NET </xh4> Требуется подключить пространство имен System.
Exception (базовый класс исключения)
Свойства:
e.Message - текстовое описание ошибки,
e.StackTrace - последовательность вызовов функций, которая привела к исключению
ApplicationException
Все пользовательские исключения
SystemException
AccessViolationException (несанкционированный доступ к памяти)
ArgumentException (один из передаваемых методу аргументов является недопустимым)
ArgumentNullException
ArgumentOutOfRangeException
ArithmeticException
DivideByZeroException (целочисленное деление на 0)
IndexOutOfRangeException
InvalidCastException (явное приведение к неправильному типу)
FormatException (данные не соответствуют формату или форматная строка неправильная)
NullReferenceException (попытка воспользоваться методом, полем или свойством через NULL-ссылку)
OutOfMemoryException
StackOverflowException
NotImplementedException (метод не реализован)
NotSupportedException (метод не поддерживается)
System.Collections.Generic.KeyNotFoundException
System.IO.IOException (пространство имен System.IO)
System.IO.FileNotFoundException
System.IO.EndOfStreamException (попытка чтения за концом потока)
Секции обработки исключений в блоке try
Полный синтаксис блока try выглядит так:
try
...
except
on e: Exception1 do
<оператор>;
on e: Exception2 do
<оператор>;
...
[else <оператор>]
end;
Вопрос: надо ли обрабатывать все возникшие исключения?
Ответ: надо обрабатывать только те, которые понятно, как обрабатывать в данном месте программы. Остальные — не обрабатывать, а считать, что это должен сделать вызывающий код.
Пример 1.
procedure DoAnything(fName: string);
begin
var f: text;
assign(f, fName);
reset(f);
...
end;Вопрос: надо ли в данном контексте обрабатывать исключение FileNotFinfException?
Попробуем обработать:
try
reset(f);
...
except
// <ничего>
end;Замечание. Обычно, тот, кто пишет код подпрограммы, которая может генерировать исключение, не знает, что с этими исключениями делать. А тот, кто вызывает — знает.
Поэтому обрабатывать исключение следует только в том месте, где уже известно, что надо делать (в нашем примере — в коде, вызывающем процедуру DoAnything).
Примечание. Раньше мы пользовались Assert:
var f: text;
Assert(FileExists(fName));
...Недостаток этого способа состоит в том, что конкретное исключение FileNotFoundException заменяется на общее AssertionException, что плохо.
В более развитых средах, как мы уже знаем, вызов Assert не генерируется в версии Release, а только в версии Debug (при разработке). Поэтому в коде могут быть оставлены как Assert, так и обработчики специфических исключений (в версии Debug будет срабатывать Assert, а в версии Release — обработчик исключения).
Пример 2.
function MyMod(a, b: integer): integer;
begin
Result := a - (a div b)*b;
end;
try
readln(a, b);
writeln(MyMod(a, b) div (a-1));
except
on FormatException do
..
on DivideByZeroException do
..
end;Замечание. Деление на ноль может возникнуть дважды: в функции MyMod и в основной программе.
Вопрос: хотим ли мы отличать эти исключения?
Создание индивидуального класса исключения. Генерация исключений при обработке исключений
Создадим свой класс исключения MyModException, унаследовав его от класса исключений приложений ApplicationException:
uses System;
type
MyModException = class(ApplicationException)
end;
function MyMod(a, b: integer): integer;
begin
try
Result := a - (a div b)*b;
except
raise new MyModException;
end;
end;
begin
var a, b: integer;
try
readln(a, b);
writeln(MyMod(a, b) div (a-1));
except
on FormatException do
writeln('Неверный формат чисел a, b');
on MyModException do
writeln('Ошибка в функции MyMod');
on DivideByZeroException do
writeln('Ошибка деления на ноль в основной программе');
end;
end.Возможен и другой вариант. Сделаем MyModException наследником класса DivideByZeroException:
type
MyModException = class(DivideByZeroException)
end;Это позволит сделать следующее: если нужно обработать любые исключения типа «деление на ноль», то достаточно написать обработчик
on DivideByZeroException doВ данном случае
try
readln(a, b);
writeln(MyMod(a, b) div (a-1));
except
on FormatException do
writeln('Неверный формат чисел a, b');
on DivideByZeroException do
writeln('Ошибка деления на ноль');
end;в секции
on DivideByZeroException doобрабатываются все исключения-наследники DivideByZeroException, в том числе MyModException.
Вопрос: в каком порядке следует писать обработчики исключений наследников и предков?
Правило. Вначале записываются обработчики классов-потомков, а потом — классов-предков.
Именно поэтому, если и писать
on Exception doто только последним обработчиком.
Замечание. Класс исключения может не быть таким простым. Его можно корректировать в соответствии с уже известными правилами наследования.
Полиморфизм и виртуальные методы
Вводные понятия
Для объектно-ориентированного программирования часто приводят следующую формулу:
ООП = инкапсуляция + наследование + полиморфизм
Рассмотрим последнюю часть этой формулы - полиморфизм.
- Полиморфизм дословно означает многообразие форм.
Более точно, полиморфизм — это способность родственных классов выполнять действия с одинаковыми именами сходным образом.
Пример.
Есть класс
Студент
Готовиться_к_экзамену()
И два его наследника:
Хороший_студент
Готовиться_к_экзамену()
и
Плохой студент
Готовиться_к_экзамену()
Действие Готовиться_к_экзамену() они выполняют по-разному.
Рассмотрим следующий код:
var p: Person;
p := new Student('Иванов', 17, 1, 11);
p.Print();Вопрос: какой метод Print вызовется?
Ответ: В разных языках программирования вызовутся Print разных классов:
- в таких языках, как Java, Eiffel — Student.Print
- а в C++, C#, PasacalABC.NET — Person.Print
Т.о. в PascalABC.NET вызовется метод Person.Print, но, хотелось бы, чтобы вызывался метод Student.Print.
- Если решение о том, какой метод вызывать, принимается на этапе компиляции (рано), то связывание имени метода с конкретным кодом называется ранним связыванием.
- Если же решение о том, какой метод вызывать, принимается на этапе выполнения программы (поздно), то связывание имени метода с конкретным кодом называется поздним связыванием.
Позднее связывание осущесвляется с методом того класса, на который ссылается переменная в процессе выполнения программы.
Итак, в PascalABC.NET по умолчанию реализовано раннее связывание.
Позднее связывание и виртуальные методы
Чтобы обеспечить позднее связывание в языке Pascal, соответствующие методы надо сделать виртуальными в базовом классе.
type
Person = class
...
public
...
procedure Print; virtual;
begin
WriteFormat('Имя: {0} Возраст: {1} ',
fName, fAge);
end;
end;
Student = class(Person)
...
public
procedure Print; override;
begin
inherited Print;
WriteFormat('Курс: {0} Группа: {1} ',
fCourse, fGroup);
end;
end;При переопределении виртуального метода в классе-потомке используется ключевое слово override.
Примечание. Переопределяющий виртуальный метод должен иметь те же параметры и тот же тип возвращаемого значения.
Вернемся к рассмотренному ранее коду:
var p: Person;
p := new Student('Иванов', 17, 1, 11);
p.Print();Теперь решение о том, какой метод вызывать, будет отложено до этапа выполнения, и будет вызвано Print того класса, на объект которого ссылается переменная в текущий момент (в данном случае — для Student).
Вызов виртуального метода осуществляется немного медленнее обычного метода.
Полиморфизм в объектно-ориентированных программирования реализуется через механизм виртуальных методов.
- Переменная базового класса, содержащая виртуальные методы, называется полиморфной переменной.
Она имеет статический тип (заявленный при объявлении) и динамический (тип объекта, на который она ссылается в данный момент выполнения программы).
Замечание. Обычная подпрограмма также может быть полиморфной.
Пример.
procedure Print(p: Person);
begin
p.Print(); // обращение полиморфизма
end;
...
Print(new Student(...));- Обычная подпрограмма называется полиморфной, если она содержит хотя бы один полиморфный параметр.
Виртуальные методы как блоки замены кода
Рассмотрим следующий полиморфный метод:
procedure polymorph(p: Base);
begin
p.Method1;
p.Method2;
p.Method3;
end;Напишем класс StudentInSession, унаследовав его от Base:
procedure polymorph(p: Base);
type
Base = class
public
procedure Method1; virtual; begin end;
procedure Method2; virtual; begin end;
procedure Method3; virtual; begin end;
end;
StudentInSession = class(Base)
public
procedure Method1; override;
begin
writeln('Sleep');
end;
procedure Method2; override;
begin
writeln('Eat');
end;
procedure Method3; override;
begin
writeln('Think');
end;
end;
...
polymorph(new StudentInSession);Места вызовов виртуальных методов в некотором коде могут быть заменены все одновременно с использованием следующего приема:
- Определим от базового класса, объект которого вызывает эти методы, потомка, в котором переопределим данные виртуальные методы.
- При конструировании вместо объекта базового класса создадим объект потомка и присвоим его указанной полиморфной переменной. При этом все вызовы виртуальных методов будут вызывать код для потомка.
Замечание. Код, содержащий вызовы виртуальных методов, всегда проектируется с учетом будущих изменений. При создании, в будущем, нового потомка этот код может вести себя совершенно по-другому, выполняя лишь основную роль. Поэтому мы всегда, когда пишем код с вызовами виртуальных методов, думаем о будущем.
Класс Base создавался только для того, чтобы его виртуальные методы были переопределены в потомке.
- Виртуальные методы, предназначенные для переопределения в потомке и ничего не выполняющие, называются абстрактными, а класс, их содержащий — абстрактным классом.
Объекты абстрактных классов создавать нельзя.
В соответствии с этим, сделаем наш базовый класс Base абстрактным:
type Base = class
public
procedure Method1; virtual; abstract;
procedure Method2; virtual; abstract;
procedure Method3; virtual; abstract;
end;Класс Object — неявный предок всех классов .NET
Все классы в PascalABC.NET, если не указан другой предок, наследуются от класса Object.
Т.е. и integer, и string — классы.
<xh4> Интерфейс класса Object </xh4>
Object = class
function Equals(o: Object): boolean; virtual;
function ToString: string; virtual;
function GetType: System.Type;Примечание. Как нам известно, использовать ключевые слова в качестве идентификаторов запрещено. Однако, можно использовать перед ними символ «&». Тогда можно, например, описать переменную &type.
Метод Equals
- Сравнивает текущий объект с объектом o и, если они равны, возвращает true, иначе — false.
- По умолчанию, все встроенные (а именно — размерные) типы и тип string сравниваются по значению, а все классы — по ссылке (две переменные считаются равными, если ссылаются на один объект).
Это можно изменить, переопределив метод Equals в потомке.
Метод ToString
- Возвращает строковое представление объекта.
Если не переопределен, то возвращает имя типа.
Метод GetType
- Возвращает объект типа System.Type, который характеризует тип данного объекта.
Пример 1.
var i: integer := 5;
begin
var s: string := i.ToString;
end.<xh4> Переопределение методов Equals и ToString в классах Person и Student </xh4>
type Person = class
...
public
...
function Equals(o: object): boolean;
begin
if o = nil then
Result := false
else if GetType <> o.GetType then
Result := false
else
begin
var p := Person(o);
Result := (Name = p.Name) and (Age = p.Age);
end;
end;
function ToString: string;
begin
Result := Format(
'Имя: {0} Возраст: {1} ',
fName, fAge);
end;type Student = class(Person)
...
public
...
function Equals(o: object): boolean;
begin
Result := inherited Equals(o);
if Result then
begin
var s := Student(o);
Result := (Course = s.Course) and (Group = s.Group);
end;
end;
function ToString: string;
begin
Result := inherited ToString + Format(
'Курс: {0} Группа: {1} ',
fCourse, fGroup);
end;Полный текст новой версии классов Person и Student
Пример 2. Родословная переменной.
uses University;
procedure PrintLineage(o: object);
begin
var t := o.GetType;
writeln(t.Name);
repeat
t := t.BaseType;
if t = nil then
exit;
writeln(t.Name);
until false;
end;
begin
var s := new SeniorStudent('Иванов', 20, 4, 11, new Teacher('Петров'), Magister);
PrintLineage(s);
end.Замечание. Полиморфизм обеспечивает изменчивость в будущем уже откомпилированного кода за счет создания подклассов.
Цепочка виртуальности и её разрыв
Пусть у нас есть следующая иерархия наследования:
A <— B <— C procedure Print; virtual; procedure Print; override; procedure Print; override;
- Говорят, что методы A.Print, B.Print и C.Print завязаны в цепочку виртуальности.
Унаследуем от класса C класс D следующим образом:
D (C) procedure Print;
Будет предупреждение: «Укажите override или reintroduce».
Ключевое слово reintroduce служит для разрыва цепочки виртуальности.
Если написать:
... reintroduce; virtual;
то это будет началом новой цепочки виртуальности.
Алгоритм поиска в цепочке виртуальности
Интерфейсы
Интерфейс - это специальным образом оформленный легковесный класс, задающий набор требований, которые должен реализовывать обычный класс.
В интерфейс входят заголовки методов и свойства с указанием доступа. Интерфейсы близки к абстрактным классам, но не могут содержать поля.
Все методы в интерфейсах считаются публичными, уровень доступа указывать не надо.
Пример.
interface IPrintable
procedure Print;
procedure Println;
end;
interface ICoords<T>
property X: T read;
property Y: T read;
end;
interface ICloneable // стандартный, из пространства имен System
procedure Clone;
end;Интуитивно: интерфейсы - это роли, которые играют объекты классов в разных ситуациях.
Один и тот же класс может реализовывать несколько интерфейсов, один и тот же интерфейс может реализовываться совершенно различными классами.
Реализация интерфейсов
type Student = class(Person,ICloneable,IPrintable)
...
function Clone: Object;
begin
Result := new Student(Name,Age,Course,Group);
end;
procedure Print;
begin
...
end;
procedure Println;
begin
...
end;
end;
type List<T> = class(ICloneable,IPrintable)
...
end;Класс наследуется от одного класса, но может реализовывать несколько интерфейсов.
Все методы и свойства интерфейса, реализуемые классом, должны быть объявлены публичными
Совершенно разнородные классы могут реализовывать одинаковые интерфейсы.
Совместимость по := и операции is as для интерфейсов
Для интерфейсов работают те же правила совместимости по присваиванию, что и для обычных классов:
- Если класс реализует интерфейс, то переменной типа интерфейс можно присвоить объект этого класса
- Можно использовать конструкции вида p is MyClass, p as MyClass, где p - переменная типа интерфейс
Интерфейсы и полиморфизм
Все методы интерфейсов, реализуемые классами, являются виртуальными - для этого необязательно использовать virtual
Если virtual не используется, то цепочка виртуальности прерывается, если используется - продолжается:
type IShape = interface(ICoords<integer>)
procedure Draw;
procedeure Hide;
procedeure MoveTo(x,y: integer);
procedeure MoveOn(dx,dy: integer);
end;
Shape = class(IShape)
...
procedure Draw; virtual;
procedeure Hide; virtual;
end;Иерархия графических фигур - классический пример использования полиморфизма
Абстрактные методы и классы
Сделать Shape абстрактным
Полиморфные контейнеры
List<Shape> Цикл по полиморфному контейнеру
- с вызовом виртуального метода
- с вызовом индивидуального метода и использованием as
- с вызовом индивидуального метода и использованием GetType
Интерфейсы и наследование
Реализация интерфейсов является одной из форм наследования. В этой форме всегда выполняется принцип подстановки. Недостатки: все методы необходимо реализовывать с нуля Достоинства: нет "груза прошлого" - тяжеловесной реализации базовых классов, которая уже не нужна в производных. Пример с наследованием с ограничениями (круг от эллипса): реализация эллипса тяжеловесна, при реализации круга мы используем лишь часть этих возможностей.
Стандартные интерфейсы .NET
Пример 1. Интерфейс IComparable и его использование.
uses System;
type Student = class(Person,IComparable<Student>)
...
public
function CompareTo(o: Student): integer;
begin
var s := Student(o);
if (Course < s.Course) or (Course = s.Course) and (Group < s.Group) then
Result := -1
else if (Course = s.Course) and (Group = s.Group) then
Result := 0
else Result := 1;
end;
end;Пример 2. Интерфейс IComparer и его использование.
Пример 3. Написание MinElem<T>(a: array of T); where T: IComparable<T>
Методы расширения
integer.Print
write(Self)
Методы расширения и интерфейсы
uses System.Collections.Generic;
function Identity(i: integer): integer;
begin
Result := i;
end;
procedure Print<T>(ie: IEnumerable<T>);
begin
foreach i: integer in ie do
write(i,' ');
writeln;
end;
begin
var a: array of integer := (1,5,3,10,7,4,8,3,11,2,2,3,4);
var a1: array of integer := (2,5,7,4,11,9,23,34);
writeln(a.All(Odd));
writeln(a.Any(Odd));
writeln(a.Average());
writeln(a.Contains(10));
writeln(a.Count());
writeln(a.Distinct().Count());
writeln(a.ElementAt(2));
writeln(a.ElementAtOrDefault(100));
Print(a.Concat(a1));
Print(a.Distinct());
Print(a.Except(a1));
Print(a.Intersect(a1));
Print(a.Union(a1));
Print(a.Skip(5));
Print(a.Take(5));
Print(a.TakeWhile(Odd));
Print(a.Where(Odd));
writeln(a.Where(Odd).Average());
writeln(a.Last());
writeln(a.Max());
writeln(a.Min());
var ff: System.Func<integer,integer> := f;
a.Select(Identity); // !!
writeln(a.SequenceEqual(a));
writeln(a.Sum());
a.OrderBy(Identity);
end.Лямбды
uses Arrays;
var a: array of integer := (1,2,3,5,7);
begin
a := a.Select((x: integer)->x*x).ToArray();
a.Writeln;
end.uses Core,Arrays;
var a: array of string := ('Hello','Abracadabra','Hi','Good','Bye');
begin
var res := a.OrderBy((x: string) -> x.Length);
res.ToArray().Writeln();
end. writeln(a.First((x: integer) -> x>5));