Основы программирования — Осенний семестр; Михалкович С.С.; 2008; II

Оператор присваивания :=

Синтаксис

<переменная> := <выражение>

Пример использования оператора присваивания.

a := (3 + 5) * 8; 
b := a + 2;

Семанитика

Вычисляется выражение в правой части, при этом, вместо имен переменных подставляются их значения.
Затем результат вычисления записывается в переменную в левой части.

Ограничение. Тип выражения должен быть совместим по присваиванию с переменной.
Например:

• одинаковые типы совместимы.
• выражение типа integer можно присвоить переменной типа real. Обратное неверно.

Операторы присваивания += и *=

Пример.

d += 1; //прибавить 1 к d
d *= 2; //умножить d на 2

Примеры использования :=

Пример 1. Перемена местами двух значений. Дано: x, y;

var x, y: integer;
begin
  read(x,y);
  var v := x;
  x := y;
  y := v;
  writeln(x, ' ', y);
end.

Это стандартное решение. В PascalABC.NET на основе этого алгоритма определена стандартная процедура Swap(x, y).

Однако, существуют и другие решения. Например:

var x, y: integer;
begin
  read(x, y);
  x := x + y;
  y := x - y;
  x := x - y;
  writeln (x, ' ', y);
end.

Пример 2. Использование промежуточных переменных в вычислениях Дано: x: real; Найти: x¹⁵;

Решение 1.

y := x * x;
z := y * y;
t := z * z;
p := t * z;
q := p * x * y;

Решение 2.

y := x * x;
z := y * x;
t := z * y;
p := t * t * t;

Решение 3.

y := x * x;
x := x * y * y;
t := x * x * x;

Заметим, что в первом решении используется 6 операций умножения, в во 2м и 3м — 5. Возникает задача: найти xⁿ за минимальное число умножений.
Об этом читай тему.

Оператор ввода

Синтаксис

read (<список переменных>) | readln (<список переменных>)

Семантика

Происходит считывание данных с клавиатуры и запись их в переменные из <списка переменных>. Вводить данные нужно либо через пробел, либо по нажатию <Enter>, при этом программа не перейдет к выполнению следующего оператора, пока не будут считаны все данные.

С процедурой ввода связан ряд ошибок (например, если переменная используется в качестве делителя, и вводится 0, или, если должно быть получено целое число, а вводится 'ABC'). Эти ошибки нужно уметь обрабатывать.

Оператор try/except и обработка ошибок ввода

Операторы, которые могут получать ошибку, заключаются специальный охранный блок - оператор try.

Синтаксис

try
  ...
  readln(a);
  ...
except
  <обработка ошибки>
end;
<продолжение работы>

Семантика

Если внутри блока try происходит ошибка выполнения, то все последующие операторы в блоке игнорируются, и выполнение программы переходит к блоку except. По выходе из except программа продолжает работу.

Если ошибки не происходит, то выполняются все операторы в блоке try, блок except не выполняется, и программа продолжает работу.

Оператор вывода

Синтаксис

write(<список выражений>) | writeln(<список выражений>)

Семантика

Выражения в списке вычисляются, и их значения выводятся на экран.
В случае writeln после вывода осуществляется переход на новую строку.

Форматы вывода

После каждого выражения в списке вывода можно использовать формат вывода в виде :a, где a — выражение целого типа.
После вещественного типа — :a:b (a задает ширину поля вывода (выравнивание по правому краю), b — количество знаков в дробной части).

Вывод с помощью write[ln]Format

writelnFormat('<форматная строка>', <список выражений>)

Пример вывода с использованием форматной строки.

writelnFormat('{0} * {1} = {2}', a, b, a * b)

Будет выведено:

a * b = a * b

В форматной строке тоже можно использовать формат вывода.
{0, 10}: 10 — это ширина поля вывода
{0, 10:f3}: 3 — это количество знаков в дробной части для вещественного числа (показывает это спецификатор f).

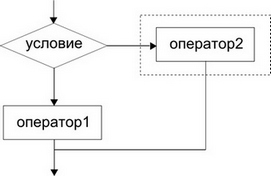
Условный оператор

Синтаксис

if <условие> then <оператор1>
             else <оператор2>

Семантика

Примеры использования для решения задач

Пример 1. Нахождение минимума
Дано: x, y;
Найти: min;

if x > y then
  min := y
else
  min := x;

Пример 2. Упорядочение a, b по возрастанию.
Ясно, что если a > b, — нужно поменять их местами.
Но тут одним оператором не обойтись. Для этого можно использовать составной оператор — один или больше операторов, заключенных в операторные скобки begin - end;:

if a > b then
begin
  var v := b;
  b := a;
  a := v;
end;

Пример 3. Вычисление функции по взаимоисключающим веткам
<math>y = \begin{cases} x, & x < 2 \\ x^2, & 2 < x < 3 \\ 1-x, & x \ge\; 3 \end{cases}</math>

if x < 2 then
  y := x
else
  if x < 3 then
    y := x * x
  else
    y := 1 - x;

Замечание. Если по ветви else располагается другой оператор if, то говорят, что возникает цепочка вложенных операторов if.

Пример 4. Найти среднее среди a, b, c (a, b, c попарно не равны)
Эта задача имеет несколько вариантов решения.

if a < b then
  if a < c then
    if b < c then
      sr := b
    else
      sr := c
  else
    sr := a
else
  if a > c then
    if b > c then
      sr := b
    else
      sr := c
  else sr := a;

Очевидно, это не самое лучшее решение.
Можно воспользоваться стандартными функциями сравнения.

sr := min(a,b);
if sr < c then
  sr := min(max(a,b), c);

Самостоятельно.

• Даны координаты вершин треугольника и точка M. Принадлежит ли M треугольнику.
• Является ли 4-угольник ABCD корректно заданным.

Арифметические выражения

Основные сведения

Каждое выражение имеет тип. Выражение называется арифметическим, если его тип — числовой. Выражение строится посредством операций( унарных или бинарных ) и операндов.

В арифметических выражениях если a и b — одного типа, то и a op b принадлежит к тому же типу. Исключением является операция "/":

a / b — вещественное.

Если a и b принадлежат к различным тиапм, то выражение принадлежит к "старшему" типу.
Например:

byte < integer < int64
integer < real

В арифметические выражения могут входить стандартные функции:

exp(x)

ln(x)

abs(x) // модуль x

sin(x)

cos(x)

sqr(x) // квадрат x

sqrt(x) // корень из x

min(x,y)

max(x,y)

pow(x,y) // x в степени y

Порядок выполнения операций в арифметических выражениях

• Операции с большим приоритетом выполняются первыми
• Функции вычисляются до операций
• Выражение в скобках вычисляется раньше
• Операции с одинаковым приоритетом выполняются слева направо, если идут подряд.

Операции div и mod для целых

x div y = x / y, округленное до ближайшего целого по направлению к нулю. Это результат от целочисленного деления.
x mod y = x - (x div y) * y. Это остаток от целочисленного деления.

Пример использования
Целочисленные операции часто применяются для определения четности числа:

x mod 2 = 0   <->   x — четное
x mod 2 <> 0   <->   x — нечетное

Логические выражения

Основные сведения

Выражение назывется логическим, если оно имеет тип boolean.
Пример.

x < 0
a >= b
a <> 3

Это простые логические выражения. Однако, с помщью логических операций можно составлять сложные.

( бинарные )   ( унарные )
  a and b         not a
  a or b
  a xor b

Таблицы истинности логических операций

a | b | a and b | a or b | a xor b 

T | T |    T    |   T    |    F
T | F |    F    |   T    |    T
F | T |    F    |   T    |    F
F | F |    F    |   F    |    T

Сокращение вычислений логических выражений

Большинство современных компиляторов, в т.ч. PascalABC.NET производит сокращенное вычисление логических выражений.
Это означает, что в выражении

a and b

если a — ложно, то b не вычисляется, а в

a or b

если a — истинно, b не вычисляется.

Это очень полезно при вычислении таких выражений, как, например,

( y <> 0 ) and (x / y > 0 )

Логически здесь все верно, однако, если бы не использовалось сокращенное вычисление, в случае равенства нулю y возникала бы ошибка деления на ноль.

Логические переменные

Можно описывать логические переменные ( тип boolean ). Им можно присваивать логические выражения.
Эти переменные принимают одно из двух возможных значений:

true ( истина )

false ( ложь )

Пример использования логических переменных

Дано: прямоугольник со сторонами, параллельными осям координат, задан координатами абсцисс вертикальных сторон ( x1, x2 ) и ординатами горизонтальных ( y1, y2 ); точка M( x, y );

Найти: находится точка внутри прямоугольника, снаружи, или лежит на границе;

var inside, outside, bound: boolean;
begin
  inside := (x > x1) and (x < x2) and (y > y1) and (y < y2);
  outside := (x < x1) or (x > x2) or (y < y1) or (y > y2);
  bound := not inside and not outside;
end.

Побитовые операции

Побитовые операции and, or, xor

Замечание. Работают только с целыми.

Смысл такой — каждое целое переводится в двоичную систему счисления и производится побитовое применение этих операций.
Пример

5 and 10

5₁₀ = 101₂
7₁₀ = 111₂

101
   ( and )
111
———
1012 = 510

Операции shl и shr

Побитовый сдвиг влево и сдвиг вправо соответственно.

shl

x shl n = x * 2n

Сдвигает двоичное представление x на n позиций влево.

shr

x shr n = x div 2n

Сдвигает двоичное представление x на n позиций вправо.

Примеры

x = 510 = 1012

x shl 2 = <—(2)101
             101002 = 2010

x shr 2 = 101—>(2)
          0012 = 110

Таблица приоритетов операций языка Object Pascal

1. унарные + - not
2. имеющие смысл умножения * / div mod and shl shr
3. имеющие смысл сложения + - or xor
4. операции отношения <> <= >= < > in

Оператор case выбора варианта

Синтакстис

case <переключатель> of
  {<список выбора>: <оператор>;}
  [else <оператор>[;]]
end

Семантика

Вначале вычисляется выражение-переключатель, после чего его значение ищется в одном из <списков выбора>.
Если значение попадает в какой-то <список выбора>, то выполняется соответствующий ему оператор, иначе, если есть ветвь else, то выполняется оператор по ветке else.

Ограничения

• выражение-переключатель должно иметь так называемый порядковый тип:

целый

символьный

перечислимый

НО НЕ строковый или вещественный.

• значения в <списках выбора> не должны пересекаться.

Примеры использования оператора выбора

Пример 1. День недели

case DayOfWeek of
  1..5: writeln('Будний');
  6,7: writeln('Выходный');
  else writeln('Ошибка');
end;

Пример 2. Цифра или буква

var c: char;
read(c);
case c of
  '0'..'9': writeln('Цифра');
  'A'..'Z', 'a'..'z', 'а'..'я', 'А'..'Я', 'ё', 'Ё': writeln('Буква');
end;

Лекция 5

Циклы с предусловием (while) и постусловием (repeat)

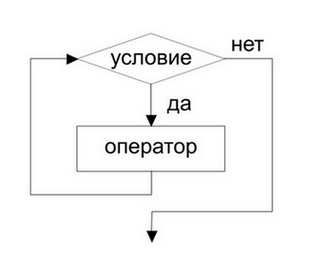
Синтаксис цикла while

while <условие> do   <— заголовок цикла
  <оператор>   <— тело цикла

<условие>::= <логическое выражение>

Семантика цикла while

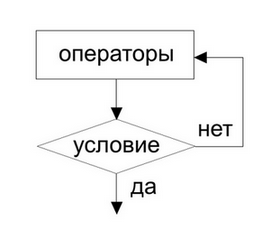
Синтаксис цикла repeat

repeat
  <операторы>
until <условие>

Семантика цикла repeat

Зацикливание

Зацикливание происходит, если:

• условие цикла с предусловием всегда истинно

Пример

while true do
  <оператор>

• условие цикла с постусловием всегда ложно

Пример

repeat
  <операторы>
until false

Итерация — однократное повторение тела цикла

Отличия между циклами while и repeat

while

тело может не выполниться ни разу

repeat

тело выполнится хотя бы один раз

Примеры

Пример 1. Сумма нечетных двузначных чисел

С использованием while

s := 0; x := 11;
while x < 100 do
begin
  s += x;
  x += 2;
end;

С использованием repeat

s := 0; x := 11;
repeat
  s += x;
  x += 2;
until x = 99;

Пример 2. Факториал

С использованием repeat

var n: integer;
read(n);
var x := n;
var p :=1;

repeat
  p *= x;
  x -= 1;
until x = 1;

С использованием while

var n: integer;
read(n);
var x := n;
var p :=1;

while x > 1 do
begin
  p *= x;
  x -= 1;
end;

Моделирование repeat с помощью while

repeat             Op
  Op       ——>     while not A do
until A;           begin
                     Op
                   end;

Моделирование while с помощью repeat

while A do         if A then
  Op         ——>     repeat
                       Op
                     until not A

Оператор цикла с параметром (for)

Синтаксис

<заголовок цикла>
  <тело цикла>

<заголовок цикла> ::= for <переменная>:=<выражение1> <направление> <выражение2> do
<тело цикла> ::= <оператор> 
<направление> ::= to | downto

Семантика

var b := <выражение1>;
var e := <выражение2>;
  <переменная> := b;
 
while <переменная> <> e do
begin
  <оператор>
  <получить следующее значение переменной>
  <переменная> += 1; | <переменная> -= 1;
end;

<получить следующее значение переменной> ::= <переменная> += 1; | <переменная> -= 1;

Ограничения:

• выражения 1 и 2 должны быть совместимы по присваиванию с переменной
• переменная должна иметь порядковый тип ( такой же, как и в case — целый, символьный или перечислимый )
• переменная цикла for не должна меняться внутри цикла for
• переменная цикла for должна быть описана в той же п/п, где используется цикл

Дополнительные возможности PascalABC.NET

Возможно описание переменной цикла в его заголовке:

for [var] i: integer := 1 to 5 do
  <оператор>

Возможно автоопределение типа при описании:

for var i := 1 to 5 do
  <оператор>

Переменная цикла, описанная в заголовке цикла, определена только внутри цикла. Замечание! Значение переменной цикла после завершения цикла не определено. Именно поэтому рекомендуется описывать переменную цикла в заголовке цикла.

Примеры использования циклов

Пример 1. Табулирование функции

Дана f(x) на [a; b], разбитая на N частей.

Выдать таблицу значений в точках разбиения.

Решение

var a, b: real;
var N: integer;
read(a, b, N);

assert(N <> 0);
assert(b > a);
var h := (b - a) / N;

Дальнейшее решение с помощью for:

for var i:=0 to N do
begin
  writelnFormat('{0,6:f2} {1,9:f4}', x, f(x));
  x += h;
end;

Дальнейшее решение с помощью while:

var eps := h / 2;
while x < (b + eps) do
begin
  writelnFormat('{0,6:f2} {1,9:f4}', x, f(x));
  x += h;
end;

Замечание. Вещественные числа в памяти компьютера представлены приближенно. Ошибка, которая возникает при представлении вещественного числа в памяти, называется ошибкой округления.
Ошибка, которая возникает в результате вычислений с вещественными числами называется вычислительной погрешностью.

Вывод. Вещественные числа нельзя сравнивать на равенство, можно только на больше/меньше.

Лекция 6

Рекуррентные соотношения

Говорят, что последовательность данных

x1, x2, x3,..., xn

является рекуррентной, если

xk + 1 = f( xk ), k = 1, 2, 3...

Пример 2. Вывод степеней двойки

var x := 1;
for var i:=1 to 10 do
begin
  writeln(x);
  x *= 2;
end;

Пример 3. Последовательность Фибоначчи

<math>\begin{cases} x_1 = 1, x_2 = 1 \\ x_{k+1} = x_k + x_{k-1}\end{cases}</math>

var a := 1;
var b := 1;
write(a, ' ', b, ' ');
for var i := 3 to 20 do
begin
  c := a + b;
  write(c, ' ');
  a := b;
  b := c;
end;

Пример 4. Вычисление НОД (алгоритм Евклида)

<math>\begin{cases} x_1 = a \\ x_2 = b \\ x_{k+1} = x_{k-1} mod x_k\end{cases}</math>

Решение

var a, b: integer;
read(a, b);
assert((a > 0) and (b > 0));
repeat
  c := a mod b;
  a := b;
  b := c;
until c = 0;
writeln(a);

Пример 5. Суммирование рядов (конечных и бесконечных)

• <math> \sum_{i=1}^n \frac{a^i}{i!}</math>

Найдем рекуррентную связь между a_i:

x1 = a
xi = xi-1 * a / i, i = 2, 3..

Решение

read(a, n);
x := a;
s := x;
for var i:=2 to n do
begin
  x *= a / i;
  s += x;
end;

• <math> \sum_{i=1}^\infty (-1)^i\frac{a^i}{i}</math>

Для вычисления суммы бесконечного ряда в простейшем случае используют следующий метод:

задается некоторый малый eps и сумма <math>\sum_{i=1}^\infty x_i</math> вычисляется, пока <math>|x_i| <\ eps</math>

Решение

assert((a > 0) and (a < 1));
i := 1;
s := 0;
y := -a;
repeat
  s += y / i;
  i += 1;
  y *= -a;
until abs(y / i) < eps;

Пример 6. Нахождение max в последовательности чисел

Решение

max := - real.MaxValue;
for var i:=1 to n do
begin
  read(x);
  if x > max then
    max := x;
end;

Пример 7. Разложение целого числа на простые множители

Будем делить x на p, начиная с p = 2. Если делится нацело, то p — множитель, если не делится, то увеличиваем p на 1, пока x <> 1.

Решение

read(x);
p := 2;
repeat
  if x mod p = 0 then
  begin
    write(p, ' ');
    x := x div p;
  end
  else
    p += 1;
until x = 1;

Лекция 7

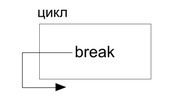
Операторы break и continue

break — оператор досрочного завершения цикла.

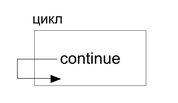
continue — оператор досрочного завершения текущей итерации цикла.

Пример 8. Поиск заданного значения среди введенных

Решение 1. С использованием оператора break

var exists: boolean := false;
for var i:=1 to n do
begin
  read(x);
  if x = k then
  begin
    exists := true;
    break;
  end;
end;

Решение 2

var i := 1;
var exists: boolean:= false;
repeat
  read(x);
  if x = k then
    exists := true;
  i += 1;
until (i > n) or exists;

Пример 9. Обработка последовательности, завершающейся нулем

Вводятся числа. Конец ввода — ноль.

Найти сумму и произвведение положительных чисел.

Решение

s := 0;
p := 1;
while True do
begin
  read(x);
  if x = 0 then
    break; 
  if x < 0 then
    continue;  //фильтр
  s += x;
  p *= x;
end;

Пример 10. Вычисление значения многочлена. Схема Горнера

Необходимо вычислить <math>\ a_0x^n + a_1x^{n-1} + ... + a_{n-1}x + a_n</math> если

a₀...a_n известны

x дано

Решение1

var p := 1.0;
var s := 0.0;
for var i:=0 to n do
begin
  read(a);
  s += p * a;
  p *= x;
end;

Это решение использует 2(n + 1) умножений.

Однако есть и другое решение — схема Горнера. Оно основана на том, что
<math>\ a_0x^2 + a_1x + a_2 = ((a_0)x + a_1)x + a_2</math>

Решение2

read(a);
var res: real := a;
for var i:=1 to n do
begin
  read(a);
  res *= x;
  res += a;
end;

Итого — всего n умножений.

Пример 11. Поиск нуля функции на отрезке

Требуется найти корень уравнения f( x ) = 0

• на отрезке [a; b]
• с заданной точностью eps
• f(x) непрерывна на этом отрезке
• имеет на нем ровно 1 корень, т.е. f(a ) * f( b ) < 0

Эта задача решается методом половинного деления.

assert(b > a);
var fa := f(a);
var fb := f(b);
assert(fa * fb < 0);

while b - a > eps do
begib
  var x := (b + a) / 2;
  var fx := f(x);
  if f(x) * f(a) > 0 then
  begin
    a := x;
    fa := fx;
  end
  else
    b := x;
end;

Лекция 8

Вложенные циклы

Метод последовательной детализации

Задача. Вывести все простые числа <= n

writeln(2);
x := 3;
while x <= n do
begin
  Если число x — простое, то
    writeln(x);
  x += 2;
end;

Метод окаймления

Задача. Вывести A^k, A = 2..10

Метод окаймления заключается в том, что что мы окаймляем данный алгоритм внешним циклом, "размораживая" некоторый параметр.

Итак, пусть A — фиксировано( "заморожено" ).

var p := 1.0;
for var i:=1 to k do
  p *= A;
write(p);

Теперь размораживаем A:

for A:=2 to 10 do
begin
  ...
end;

Переборные задачи

Класс задач, в которых требуется перебрать множество вариантов и выбрать несколько оптимальных по каким-то критериям.

Задача

Дано равенство: a² + b² = c², a,b,c — целые

Вывести все такие тройки (a, b, c), что: a<=100, b<=1000, c<=1000;

Решение

for var a:=1 to 1000 do
  for var b:=1 to 1000 do
    for var c:=1 to 1000 do
      if a*a + b*b = c*c then
        writeln(a, b, c);

Однако, ясно, что

a2 + b2 = c2 <=> b2 + a2 = c2

Оптимизация

for var a:=1 to 1000 do
  for var b:=1 to a-1 do
  begin
    var c := round(sqrt(a*a + b*b));
    if a*a + b*b = c*c then
    begin
      writeln(a, b, c);
      writeln(b, a, c);
    end;
  end;

Вывод. При наличии нескольких вложенных циклов нужно оптимизировать самый внутренний.