Основы программирования — Осенний семестр; Михалкович С.С.; 2008; II — различия между версиями
Admin (обсуждение | вклад) (→Логические выражения) |
Admin (обсуждение | вклад) (→Координаты средней точки) |
||
| (не показана 21 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
[[Категория:Основы программирования]] | [[Категория:Основы программирования]] | ||
| + | [[Страница курса Основы программирования|К основной странице курса]] | ||
== Основные операторы == | == Основные операторы == | ||
=== Оператор присваивания := === | === Оператор присваивания := === | ||
| Строка 148: | Строка 149: | ||
<br><tt>{0, 10}</tt>: 10 — это ширина поля вывода | <br><tt>{0, 10}</tt>: 10 — это ширина поля вывода | ||
<br><tt>{0, 10:f3}</tt>: 3 — это количество знаков в дробной части для вещественного числа (показывает это спецификатор <tt>'''f'''</tt>). | <br><tt>{0, 10:f3}</tt>: 3 — это количество знаков в дробной части для вещественного числа (показывает это спецификатор <tt>'''f'''</tt>). | ||
| + | <br><tt>{0, 10:e3}</tt> — экспоненциальный формат. | ||
=== Арифметические выражения === | === Арифметические выражения === | ||
| − | + | ==== Основные сведения ==== | |
Каждое выражение имеет '''тип'''. Выражение называется '''''арифметическим''''', если его тип — ''числовой''. <br /> | Каждое выражение имеет '''тип'''. Выражение называется '''''арифметическим''''', если его тип — ''числовой''. <br /> | ||
Выражение строится посредством '''''операций''''' (унарных или бинарных) и '''''операндов'''''. | Выражение строится посредством '''''операций''''' (унарных или бинарных) и '''''операндов'''''. | ||
| Строка 162: | Строка 164: | ||
integer < real | integer < real | ||
| + | ==== Стандартные функции ==== | ||
В арифметические выражения могут входить стандартные функции: | В арифметические выражения могут входить стандартные функции: | ||
'''exp'''(x) | '''exp'''(x) | ||
| Строка 170: | Строка 173: | ||
'''sqr'''(x) // квадрат x | '''sqr'''(x) // квадрат x | ||
'''sqrt'''(x) // корень из x | '''sqrt'''(x) // корень из x | ||
| + | '''round'''(x) - целое, полученное в результате округления вещественного x | ||
| + | '''trunc'''(x) - целое, полученное в результате отбрасывания дробной части у вещественного x | ||
'''min'''(x,y) | '''min'''(x,y) | ||
'''max'''(x,y) | '''max'''(x,y) | ||
| − | ''' | + | '''power'''(x,y)// x в степени y |
| + | '''random'''(n)// псевдослучайное целое число от 0 до n-1 | ||
| + | '''random'''(a,b)// псевдослучайное целое число от a до b | ||
<xh4> Порядок выполнения операций в арифметических выражениях </xh4> | <xh4> Порядок выполнения операций в арифметических выражениях </xh4> | ||
| Строка 188: | Строка 195: | ||
x '''mod''' 2 = 0 <-> x — четное | x '''mod''' 2 = 0 <-> x — четное | ||
x '''mod''' 2 <> 0 <-> x — нечетное | x '''mod''' 2 <> 0 <-> x — нечетное | ||
| + | |||
| + | === Логические выражения === | ||
| + | <xh4> Основные сведения </xh4> | ||
| + | Выражение назывется '''логическим''', если оно имеет тип <tt>'''boolean'''.</tt> <br /> | ||
| + | ''<u>Пример</u>''. | ||
| + | x < 0 | ||
| + | a >= b | ||
| + | a <> 3 | ||
| + | |||
| + | Это простые логические выражения. Однако, с помщью '''логических операций''' можно составлять сложные. | ||
| + | (бинарные) (унарные) | ||
| + | a '''and''' b '''not''' a | ||
| + | a '''or''' b | ||
| + | a '''xor''' b | ||
| + | |||
| + | <xh4> Таблицы истинности логических операций </xh4> | ||
| + | a | b | a '''and''' b | a '''or''' b | a '''xor''' b | ||
| + | |||
| + | T | T | T | T | F | ||
| + | T | F | F | T | T | ||
| + | F | T | F | T | T | ||
| + | F | F | F | F | F | ||
| + | |||
| + | <xh4> Сокращение вычислений логических выражений </xh4> | ||
| + | Большинство современных компиляторов, в т.ч. PascalABC.NET производит '''''сокращенное вычисление логических выражений'''''. <br /> | ||
| + | Это означает, что в выражении | ||
| + | a '''and''' b | ||
| + | если a — ложно, то <tt>b</tt> не вычисляется, а в | ||
| + | a '''or''' b | ||
| + | если <tt>a</tt> — истинно, <tt>b</tt> не вычисляется. | ||
| + | |||
| + | Это очень полезно при вычислении таких выражений, как, например, | ||
| + | (y <> 0) '''and''' (x / y > 0) | ||
| + | |||
| + | Логически здесь все верно, однако, если бы не использовалось сокращенное вычисление, в случае равенства нулю <tt>y</tt>'а возникала бы ошибка деления на ноль. | ||
| + | |||
| + | <xh4> Логические переменные </xh4> | ||
| + | Можно описывать логические переменные (тип <tt>'''boolean'''</tt>). Им можно присваивать логические выражения. <br /> | ||
| + | Эти переменные принимают одно из двух возможных значений: | ||
| + | :<tt>'''true'''</tt> (истина) | ||
| + | :<tt>'''false'''</tt> (ложь) | ||
| + | |||
| + | ''<u>Пример</u> использования логических переменных'' <br /> | ||
| + | Дано: прямоугольник со сторонами, параллельными осям координат, задан координатами абсцисс вертикальных сторон (<tt>x1, x2</tt>) и ординатами горизонтальных (y1, y2); точка M( x, y ); <br /> | ||
| + | Найти: находится ли точка внутри прямоугольника, снаружи, или лежит на границе; | ||
| + | |||
| + | <source lang="Pascal"> | ||
| + | var inside, outside, bound: boolean; | ||
| + | begin | ||
| + | inside := (x > x1) and (x < x2) and (y > y1) and (y < y2); | ||
| + | outside := (x < x1) or (x > x2) or (y < y1) or (y > y2); | ||
| + | bound := not inside and not outside; | ||
| + | end. | ||
| + | </source> | ||
| + | |||
| + | === Побитовые операции === | ||
| + | <xh4> Побитовые операции and, or, xor, not </xh4> | ||
| + | '''Замечание.''' Работают только с целыми. | ||
| + | |||
| + | Соответствующая операция применяется к каждому биту двоичного представления числа. <br /> | ||
| + | ''<u>Пример</u>.'' | ||
| + | 5 '''and''' 7 | ||
| + | 5<sub>10</sub> = 101<sub>2</sub> <br /> | ||
| + | 7<sub>10</sub> = 111<sub>2</sub> | ||
| + | |||
| + | 101 | ||
| + | ( '''and''' ) | ||
| + | 111 | ||
| + | ——— | ||
| + | 101<sub>2</sub> = 5<sub>10</sub> | ||
| + | |||
| + | <xh4> Операции shl и shr </xh4> | ||
| + | '''''Побитовый сдвиг влево''''' и '''''сдвиг вправо''''' соответственно. | ||
| + | |||
| + | <xh4> shl </xh4> | ||
| + | x '''shl''' n = x * 2<sup>n</sup> | ||
| + | |||
| + | Сдвигает двоичное представление <tt>x</tt> на <tt>n</tt> позиций влево. | ||
| + | |||
| + | <xh4> shr </xh4> | ||
| + | x '''shr''' n = x div 2<sup>n</sup> | ||
| + | |||
| + | Сдвигает двоичное представление <tt>x</tt> на <tt>n</tt> позиций вправо. | ||
| + | |||
| + | <xh4> Примеры </xh4> | ||
| + | x = 5<sub>10</sub> = 101<sub>2</sub> | ||
| + | |||
| + | x shl 2 = <—(<sup>2</sup>)101 | ||
| + | 10100<sub>2</sub> = 20<sub>10</sub> | ||
| + | |||
| + | x shr 2 = 101—>(<sup>2</sup>) | ||
| + | 001<sub>2</sub> = 1<sub>10</sub> | ||
| + | |||
| + | === Таблица приоритетов операций языка Object Pascal === | ||
| + | # унарные <tt>'''+ - not'''</tt> | ||
| + | # имеющие смысл ''умножения'' <tt>'''* / div mod and shl shr'''</tt> | ||
| + | # имеющие смысл ''сложения'' <tt>'''+ - or xor'''</tt> | ||
| + | # операции ''отношения'' <tt>'''<> <= >= < > in'''</tt> | ||
=== Условный оператор === | === Условный оператор === | ||
| Строка 197: | Строка 302: | ||
[[Изображение: If.jpg]] | [[Изображение: If.jpg]] | ||
| − | + | ==== Примеры использования для решения задач ==== | |
''<u>Пример 1</u>.'' Нахождение минимума | ''<u>Пример 1</u>.'' Нахождение минимума | ||
| − | <br>Дано: <tt>x, y</tt> | + | <br>Дано: <tt>x, y</tt> |
| − | <br>Найти: <tt>min</tt> | + | <br>Найти: <tt>min</tt> |
<source lang="Pascal"> | <source lang="Pascal"> | ||
| Строка 226: | Строка 331: | ||
if x < 2 then | if x < 2 then | ||
y := x | y := x | ||
| − | else | + | else if x < 3 then |
| − | + | y := x * x | |
| − | + | else y := 1 - x; | |
| − | |||
| − | |||
</source> | </source> | ||
'''Замечание.''' Если по ветви '''<tt>else</tt>''' располагается другой оператор '''<tt>if</tt>''', то говорят, что возникает '''''цепочка вложенных операторов <tt>if</tt>'''''. | '''Замечание.''' Если по ветви '''<tt>else</tt>''' располагается другой оператор '''<tt>if</tt>''', то говорят, что возникает '''''цепочка вложенных операторов <tt>if</tt>'''''. | ||
| − | ''<u>Пример 4</u>.'' | + | ====Координаты средней точки==== |
| − | + | ''<u>Пример 4</u>.'' Даны координаты трех точек на прямой <tt>a, b, c</tt> (<tt>a, b, c</tt> попарно не равны). Найти m - координаты средней точки <br /> | |
| + | |||
| + | '''Решение 1.''' | ||
| + | |||
| + | Достаточно рассмотреть случай, когда координаты точек равны 1,2 и 3 | ||
| + | |||
| + | Рассмотрим все возможные ситуации распределения этих значений между a,b,c: | ||
| + | |||
| + | a b c | ||
| + | 1 2 3 a<b | ||
| + | 1 3 2 a<b | ||
| + | 2 1 3 | ||
| + | 2 3 1 a<b | ||
| + | 3 1 2 | ||
| + | 3 2 1 | ||
| + | |||
| + | При a<b возможны три варианта, в двух из которых a<c. | ||
| + | При a>b возможны три варианта, в двух из которых a>c. | ||
| + | |||
| + | Решение представляется вложенными операторами if с уровнем вложенности 3. | ||
| + | |||
<source lang="Pascal"> | <source lang="Pascal"> | ||
if a < b then | if a < b then | ||
if a < c then | if a < c then | ||
if b < c then | if b < c then | ||
| − | + | m := b | |
else | else | ||
| − | + | m := c | |
else | else | ||
| − | + | m := a | |
else | else | ||
if a > c then | if a > c then | ||
| − | if b | + | if b < c then |
| − | + | m := c | |
else | else | ||
| − | + | m := b | |
| − | else | + | else m := a; |
</source> | </source> | ||
| − | + | По количеству операций (3 сравнения, одно присваивание) это - самое лучшее решение | |
| − | + | ||
| + | То же решение, записанное с помощью функции min: | ||
| + | |||
<source lang="Pascal"> | <source lang="Pascal"> | ||
| − | + | if a < b then | |
| − | if | + | if a < c then |
| − | + | m := min(b,c) | |
| + | else m := a | ||
| + | else | ||
| + | if a > c then | ||
| + | m := min(b,c) | ||
| + | else m := a; | ||
</source> | </source> | ||
| − | '' | + | '''Решение 2.''' |
| − | |||
| − | |||
| − | === | + | <source lang="Pascal"> |
| − | + | var m1 := min(a,b); | |
| − | + | var m2 := max(a,b); | |
| + | </source> | ||
| − | + | a b c | |
| − | + | 1 2 3 c>m2 | |
| − | + | 1 3 2 | |
| − | + | 2 1 3 c>m2 | |
| − | + | 2 3 1 c<m1 | |
| + | 3 1 2 | ||
| + | 3 2 1 c<m1 | ||
| − | + | <source lang="Pascal"> | |
| − | + | var m1 := min(a,b); | |
| − | + | var m2 := max(a,b); | |
| − | + | if c<m1 then | |
| − | + | m := m1 | |
| − | + | else if c>m2 then | |
| − | + | m := m2 | |
| − | + | else m := c; | |
| + | </source> | ||
| − | + | Данное решение менее эффективно по числу сравнений и присваиваний (посчитайте самостоятельно), но по понятности может восприниматься лучше предыдущего. | |
| − | |||
| − | + | ====Самостоятельные задания==== | |
| − | + | * Даны координаты вершин треугольника и точка M, не лежащая на границе треугольника. Принадлежит ли M треугольнику. | |
| − | + | * Является ли 4-угольник ABCD корректно заданным. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Оператор case выбора варианта === | === Оператор case выбора варианта === | ||
Текущая версия на 11:21, 14 сентября 2013
Содержание
- 1 Основные операторы
- 1.1 Оператор присваивания :=
- 1.2 Оператор ввода
- 1.3 Оператор try/except и обработка ошибок ввода
- 1.4 Оператор вывода
- 1.5 Арифметические выражения
- 1.6 Логические выражения
- 1.7 Побитовые операции
- 1.8 Таблица приоритетов операций языка Object Pascal
- 1.9 Условный оператор
- 1.10 Оператор case выбора варианта
Основные операторы
Оператор присваивания :=
<xh4> Синтаксис </xh4>
<переменная> := <выражение>
Пример использования оператора присваивания.
a := (3 + 5) * 8;
b := a + 2;<xh4> Семанитика </xh4>
Вычисляется выражение в правой части, при этом, вместо имен переменных подставляются их значения.
Затем результат вычисления записывается в переменную в левой части.
Ограничение. Тип выражения должен быть совместим по присваиванию с переменной.
Например:
- одинаковые типы совместимы.
- выражение типа integer можно присвоить переменной типа real. Обратное неверно.
<xh4> Операторы присваивания += и *= </xh4> Пример.
d += 1; //прибавить 1 к d
d *= 2; //умножить d на 2<xh4> Примеры использования := </xh4> Пример 1. Перемена местами двух значений. Дано: x, y;
var x, y: integer;
begin
read(x,y);
var v := x;
x := y;
y := v;
writeln(x, ' ', y);
end.Это стандартное решение. В PascalABC.NET на основе этого алгоритма определена стандартная процедура Swap(x, y).
Однако, существуют и другие решения. Например:
var x, y: integer;
begin
read(x, y);
x := x + y;
y := x - y;
x := x - y;
writeln (x, ' ', y);
end.Пример 2. Использование промежуточных переменных в вычислениях Дано: x: real; Найти: x15;
Решение 1.
y := x * x;
z := y * y;
t := z * z;
p := t * z;
q := p * x * y;Решение 2.
y := x * x;
z := y * x;
t := z * y;
p := t * t * t;Решение 3.
y := x * x;
x := x * y * y;
t := x * x * x;Заметим, что в первом решении используется 6 операций умножения, в во 2м и 3м — 5. Возникает задача: найти xn за минимальное число умножений.
Об этом читай тему.
Оператор ввода
<xh4> Синтаксис </xh4>
read (<список переменных>) | readln (<список переменных>)
<xh4> Семантика </xh4> Происходит считывание данных с клавиатуры и запись их в переменные из <списка переменных>. Вводить данные нужно либо через пробел, либо по нажатию <Enter>, при этом программа не перейдет к выполнению следующего оператора, пока не будут считаны все данные.
Имеются также стандартные функции ReadInteger, ReadReal, ReadlnInteger, ReadlnReal:
var n := ReadInteger;
var r := ReadlnReal;С процедурой ввода связан ряд ошибок времени выполнения (например, если переменная используется в качестве делителя, и вводится 0, или, если должно быть получено целое число, а вводится 'ABC'). Эти ошибки нужно уметь обрабатывать.
Оператор try/except и обработка ошибок ввода
Операторы, которые могут получать ошибку, заключаются специальный охранный блок - оператор try.
<xh4> Синтаксис </xh4>
try
...
readln(a);
...
except
<обработка ошибки>
end;
<продолжение работы><xh4> Семантика </xh4> Если внутри блока try происходит ошибка выполнения, то все последующие операторы в блоке игнорируются, и выполнение программы переходит к блоку except. По выходе из except программа продолжает работу.
Если ошибки не происходит, то выполняются все операторы в блоке try, блок except не выполняется, и программа продолжает работу.
Оператор вывода
<xh4> Синтаксис </xh4>
write(<список выражений>) | writeln(<список выражений>)
<xh4> Семантика </xh4>
Выражения в списке вычисляются, и их значения выводятся на экран.
В случае writeln после вывода осуществляется переход на новую строку.
<xh4> Форматы вывода </xh4>
После каждого выражения в списке вывода можно использовать формат вывода в виде :a, где a — выражение целого типа.
После вещественного типа — :a:b (a задает ширину поля вывода (выравнивание по правому краю), b — количество знаков в дробной части).
<xh4> Вывод с помощью write[ln]Format </xh4>
writelnFormat('<форматная строка>', <список выражений>)
Пример вывода с использованием форматной строки.
writelnFormat('{0} * {1} = {2}', a, b, a * b)Будет выведено:
a * b = a * b
В форматной строке тоже можно использовать формат вывода.
{0, 10}: 10 — это ширина поля вывода
{0, 10:f3}: 3 — это количество знаков в дробной части для вещественного числа (показывает это спецификатор f).
{0, 10:e3} — экспоненциальный формат.
Арифметические выражения
Основные сведения
Каждое выражение имеет тип. Выражение называется арифметическим, если его тип — числовой.
Выражение строится посредством операций (унарных или бинарных) и операндов.
В арифметических выражениях если a и b — одного типа, то и a op b принадлежит к тому же типу. Исключением является операция "/":
- a / b — вещественное.
Если a и b принадлежат к различным типам, то выражение принадлежит к "старшему" типу.
Например:
byte < integer < int64 integer < real
Стандартные функции
В арифметические выражения могут входить стандартные функции:
exp(x) ln(x) abs(x) // модуль x sin(x) cos(x) sqr(x) // квадрат x sqrt(x) // корень из x round(x) - целое, полученное в результате округления вещественного x trunc(x) - целое, полученное в результате отбрасывания дробной части у вещественного x min(x,y) max(x,y) power(x,y)// x в степени y random(n)// псевдослучайное целое число от 0 до n-1 random(a,b)// псевдослучайное целое число от a до b
<xh4> Порядок выполнения операций в арифметических выражениях </xh4>
- Операции с большим приоритетом выполняются первыми
- Функции вычисляются до операций
- Выражение в скобках вычисляется раньше
- Операции с одинаковым приоритетом выполняются слева направо, если идут подряд.
<xh4> Операции div и mod для целых </xh4>
x div y = x / y, округленное до ближайшего целого по направлению к нулю. Это результат от целочисленного деления.
x mod y = x - (x div y) * y. Это остаток от целочисленного деления.
Пример использования
Целочисленные операции часто применяются для определения четности числа:
x mod 2 = 0 <-> x — четное x mod 2 <> 0 <-> x — нечетное
Логические выражения
<xh4> Основные сведения </xh4>
Выражение назывется логическим, если оно имеет тип boolean.
Пример.
x < 0 a >= b a <> 3
Это простые логические выражения. Однако, с помщью логических операций можно составлять сложные.
(бинарные) (унарные) a and b not a a or b a xor b
<xh4> Таблицы истинности логических операций </xh4>
a | b | a and b | a or b | a xor b T | T | T | T | F T | F | F | T | T F | T | F | T | T F | F | F | F | F
<xh4> Сокращение вычислений логических выражений </xh4>
Большинство современных компиляторов, в т.ч. PascalABC.NET производит сокращенное вычисление логических выражений.
Это означает, что в выражении
a and b
если a — ложно, то b не вычисляется, а в
a or b
если a — истинно, b не вычисляется.
Это очень полезно при вычислении таких выражений, как, например,
(y <> 0) and (x / y > 0)
Логически здесь все верно, однако, если бы не использовалось сокращенное вычисление, в случае равенства нулю y'а возникала бы ошибка деления на ноль.
<xh4> Логические переменные </xh4>
Можно описывать логические переменные (тип boolean). Им можно присваивать логические выражения.
Эти переменные принимают одно из двух возможных значений:
- true (истина)
- false (ложь)
Пример использования логических переменных
Дано: прямоугольник со сторонами, параллельными осям координат, задан координатами абсцисс вертикальных сторон (x1, x2) и ординатами горизонтальных (y1, y2); точка M( x, y );
Найти: находится ли точка внутри прямоугольника, снаружи, или лежит на границе;
var inside, outside, bound: boolean;
begin
inside := (x > x1) and (x < x2) and (y > y1) and (y < y2);
outside := (x < x1) or (x > x2) or (y < y1) or (y > y2);
bound := not inside and not outside;
end.Побитовые операции
<xh4> Побитовые операции and, or, xor, not </xh4> Замечание. Работают только с целыми.
Соответствующая операция применяется к каждому биту двоичного представления числа.
Пример.
5 and 7
510 = 1012
710 = 1112
101 ( and ) 111 ——— 1012 = 510
<xh4> Операции shl и shr </xh4> Побитовый сдвиг влево и сдвиг вправо соответственно.
<xh4> shl </xh4>
x shl n = x * 2n
Сдвигает двоичное представление x на n позиций влево.
<xh4> shr </xh4>
x shr n = x div 2n
Сдвигает двоичное представление x на n позиций вправо.
<xh4> Примеры </xh4>
x = 510 = 1012
x shl 2 = <—(2)101
101002 = 2010
x shr 2 = 101—>(2)
0012 = 110
Таблица приоритетов операций языка Object Pascal
- унарные + - not
- имеющие смысл умножения * / div mod and shl shr
- имеющие смысл сложения + - or xor
- операции отношения <> <= >= < > in
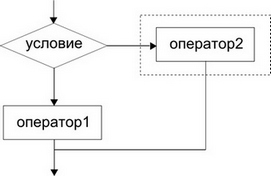
Условный оператор
<xh4> Синтаксис </xh4>
if <условие> then <оператор1>
[else <оператор2>]
Примеры использования для решения задач
Пример 1. Нахождение минимума
Дано: x, y
Найти: min
if x > y then
min := y
else
min := x;Пример 2. Упорядочение a, b по возрастанию.
Ясно, что если a > b, — нужно поменять их местами.
Но тут одним оператором не обойтись.
Для этого можно использовать составной оператор — один или больше операторов, заключенных в операторные скобки begin - end;:
if a > b then
begin
var v := b;
b := a;
a := v;
end;Пример 3. Вычисление функции по взаимоисключающим веткам
<math>y = \begin{cases} x, & x < 2 \\ x^2, & 2 < x < 3 \\ 1-x, & x \ge\; 3 \end{cases}</math>
if x < 2 then
y := x
else if x < 3 then
y := x * x
else y := 1 - x;Замечание. Если по ветви else располагается другой оператор if, то говорят, что возникает цепочка вложенных операторов if.
Координаты средней точки
Пример 4. Даны координаты трех точек на прямой a, b, c (a, b, c попарно не равны). Найти m - координаты средней точки
Решение 1.
Достаточно рассмотреть случай, когда координаты точек равны 1,2 и 3
Рассмотрим все возможные ситуации распределения этих значений между a,b,c:
a b c 1 2 3 a<b 1 3 2 a<b 2 1 3 2 3 1 a<b 3 1 2 3 2 1
При a<b возможны три варианта, в двух из которых a<c. При a>b возможны три варианта, в двух из которых a>c.
Решение представляется вложенными операторами if с уровнем вложенности 3.
if a < b then
if a < c then
if b < c then
m := b
else
m := c
else
m := a
else
if a > c then
if b < c then
m := c
else
m := b
else m := a;По количеству операций (3 сравнения, одно присваивание) это - самое лучшее решение
То же решение, записанное с помощью функции min:
if a < b then
if a < c then
m := min(b,c)
else m := a
else
if a > c then
m := min(b,c)
else m := a;Решение 2.
var m1 := min(a,b);
var m2 := max(a,b);a b c 1 2 3 c>m2 1 3 2 2 1 3 c>m2 2 3 1 c<m1 3 1 2 3 2 1 c<m1
var m1 := min(a,b);
var m2 := max(a,b);
if c<m1 then
m := m1
else if c>m2 then
m := m2
else m := c;Данное решение менее эффективно по числу сравнений и присваиваний (посчитайте самостоятельно), но по понятности может восприниматься лучше предыдущего.
Самостоятельные задания
- Даны координаты вершин треугольника и точка M, не лежащая на границе треугольника. Принадлежит ли M треугольнику.
- Является ли 4-угольник ABCD корректно заданным.
Оператор case выбора варианта
<xh4> Синтакстис </xh4>
case <переключатель> of
{<список выбора>: <оператор>;}
[else <оператор>[;]]
end
<xh4> Семантика </xh4>
Вначале вычисляется выражение-<переключатель>, после чего его значение ищется в одном из <списков выбора>.
Если значение попадает в какой-то <список выбора>, то выполняется соответствующий ему оператор, иначе, если есть ветвь else, то выполняется оператор по ветке else.
<xh4> Ограничения </xh4>
- выражение-переключатель должно иметь так называемый порядковый тип:
- целый
- символьный
- перечислимый
НО НЕ строковый или вещественный.
- значения в <списках выбора> не должны пересекаться.
<xh4> Примеры использования оператора выбора </xh4> Пример 1. День недели
case DayOfWeek of
1..5: writeln('Будний');
6, 7: writeln('Выходный');
else writeln('Ошибка');
end;Пример 2. Цифра или буква
var c: char;
read(c);
case c of
'0'..'9': writeln('Цифра');
'A'..'Z', 'a'..'z', 'а'..'я', 'А'..'Я', 'ё', 'Ё': writeln('Буква');
end;