Основы программирования — второй семестр 08-09; Михалкович С.С.; IIб часть
Содержание
Динамические структуры данных
Введение
Данные объединяются в структуры.
Мы уже знаем такие структуры данных как:
- массивы (подразумеваем статические)
- записи
Их основная проблема — фиксированный размер, определяемый на этапе компиляции.
Решением проблемы являются динамические структуры данных. Они строятся из узлов, которые, в свою очередь, состоят из данных и полей связи.
Рассмотрим такой пример:
type
Node<DataType> = class
data: DataType;
next: Node<DataType>;
constructor (d: DataType; n: Node<DataType>);
begin
data := d;
next := n;
end;
end;
begin
var p := new Node<char>('!', nil); // под объект класса Node<char> выделилась динамическая память;
// p начала указывать на эту динамическую память
end.Виды списков
- Линейный односвязный список

- Циклический односвязный список

- Двусвязный линейный список

- Циклический двусвязный список
Односвязные линейные списки
Класс узла односвязного списка
/// <summary>
/// Узел односвязного линейного списка
/// </summary>
type SNode<T> = class
public // <- для печати write
/// Поле данных
data: T;
/// Поле связи со следующим узлом
next: SNode<T>;
/// <summary>
/// Инициализирует новый экземпляр узла односвязного списка
/// со значением dt поля данных и ссылкой next на следующий узел
/// </summary>
/// <param name="dt">Значение поля данных узла</param>
/// <param name="next">Сслыка на следующий узел. По умолчанию: nil</param>
constructor(dt: T; next: SNode<T> := nil);
begin
data := dt;
self.next := next;
end;
end;
/// Умный конструктор типа SNode: вывод типа и экономия на слове new
function MkSnode<T>(dt: T; next: SNode<T> := nil) := new SNode<T>(dt, next);Стандартные операции с односвязными линейными списками
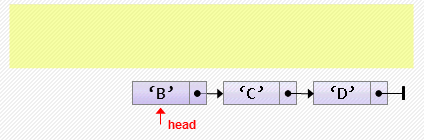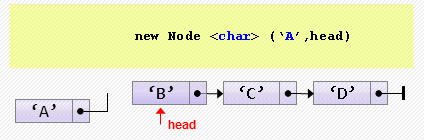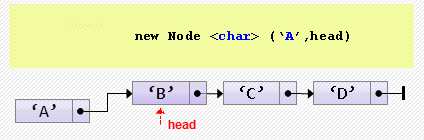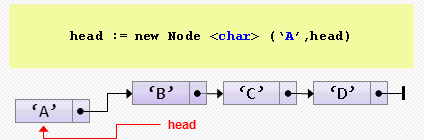
- Вставка элемента в начало
head := new Node<char>('A', head);При многократной вставке в начало элементы располагаются в обратном порядке.
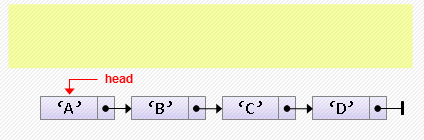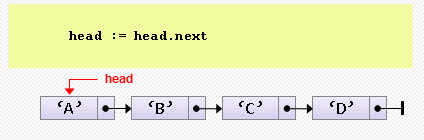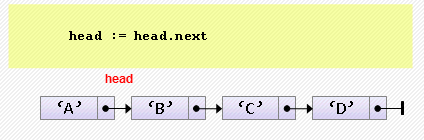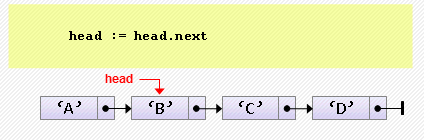
- Удаление элемента из начала
head := head.next;Если изначально список пуст, произойдет ошибка «попытка разыменования нулевого указателя». Эту ситуацию надо предусмотреть:
if head <> nil then
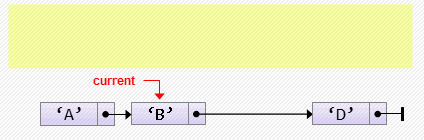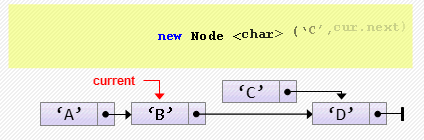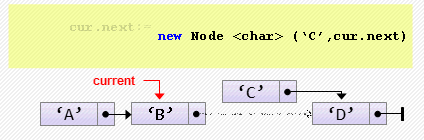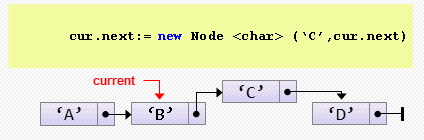
head := head.next;- Вставка элемента после текущего
cur.next := new Node<char>('C', cur.next);Если cur никуда не указывает, произойдет ошибка. Предусмотрим эту ситуацию:
if cur <> nil then
cur.next := new Node<char>('d', cur.next);Заметим также, что если cur указывает на последний элемент списка, ошибки не произойдет (фактически, будет произведена вставка в конец списка).
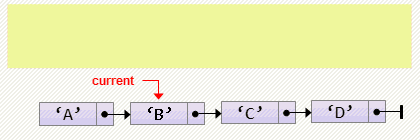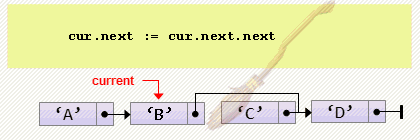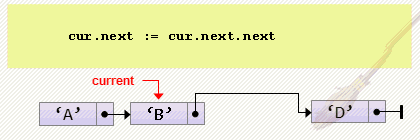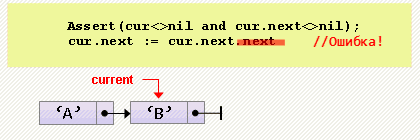
- Удаление элемента после текущего
cur.next := cur.next.next;Заметим, что текущий элемент — cur, должен не только не быть пустым, но и не быть последним в списке, т.к. происходят два разыменования: cur.next и cur.next.next. Для проверки этого факта можем воспользоваться утверждением:
Assert( (cur <> nil) and (cur.next <> nil) );
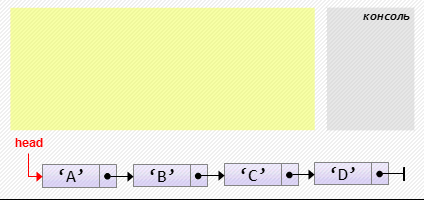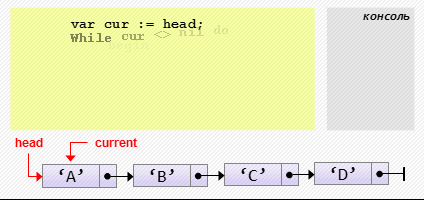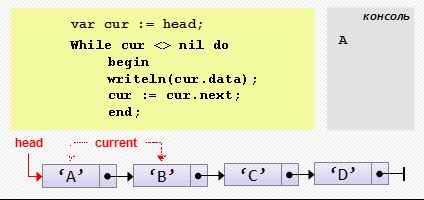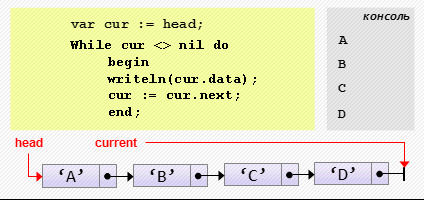
cur.next := cur.next.next;- Проход по списку
var cur := head;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.next;
end;Примеры использования
Пример 1.
Дан файл целых чисел.
Записать все его элементы в линейный односвязный список.
var f: file of integer;
Assign(f, 'numbers.dat');
Reset(f);
var a: integer;
Read(f, a);
var head := new Node<integer>(a, nil);
var cur := head;
while not Eof(f) do
begin
read(f, a);
cur.next := new Node<integer>(a, nil);
cur := cur.next;
end;
Close(f);Пример 2.
Поиск элемента с заданным значением.
// x — искомый символ
var cur := head;
while (cur <> nil) and (cur.data <> x) do
cur := cur.next;
if cur = nil then
// не найдено
else
// cur — ссылка на искомый xДвусвязные линейные списки
Класс узла двусвязного списка
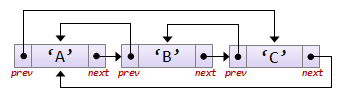
В отличие от односвязных линейных списков, двусвязные, помимо полей data и next, имеют поле prev (указатель на предыдущий элемент списка):
type
Node<T> = class
data: T;
prev, next: Node<T>;
constructor (d: T; p, n: Node<T>);
begin
data := d;
prev := p;
next := n;
end;
end;В случае двусвязного списка нам достаточно иметь ссылку на любой узел, тогда все остальные можно найти. Однако, для удобства, будем считать, что у нас есть две ссылки:
- head — на начало списка
- tail — на конец списка
Стандартные операции с двусвязными линейными списками
Замечание. При выполнении любой операции нужно следить за возможными изменениями head и tail.
- Инициализация
head := nil;
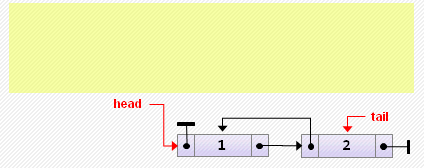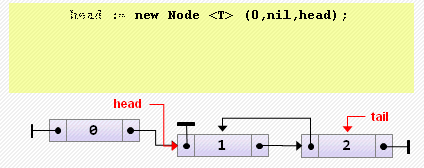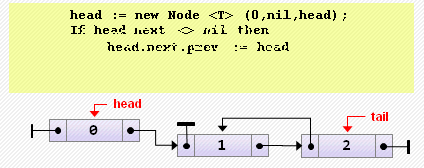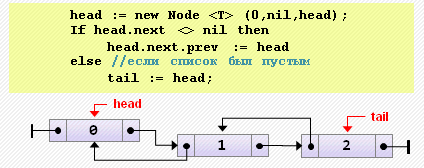
tail := nil;- Добавление элемента в начало
Примечание. Если изначально список был пуст, после добавления элемента надо не забыть сделать tail указывающим на него.
head := new Node<T>(0, nil, head);
if head.next <> nil then
head.next.prev := head
else // если список был пуст
tail := head;- Добавление элемента в конец
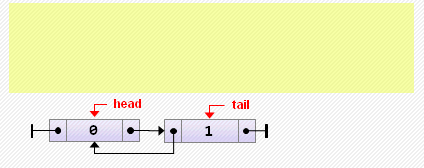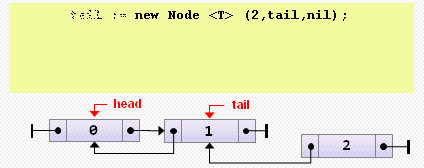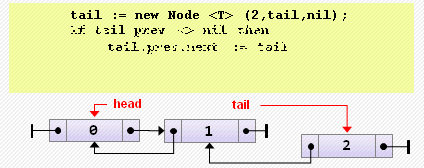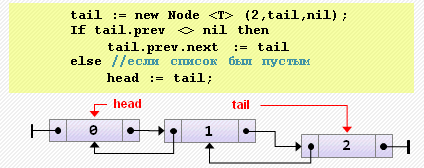
tail := new Node<T>(2, tail, nil);
if tail.prev <> nil then
tail.prev.next := tail
else // если список был пуст
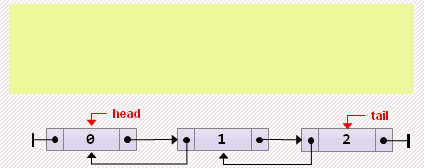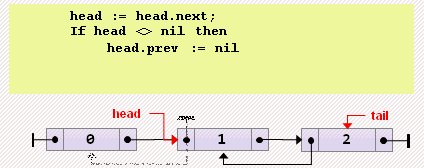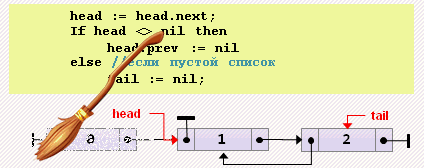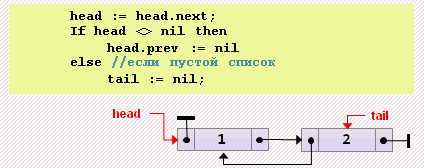
head := tail;- Удаление элемента из начала
head := head.next;
if head = nil then
tail := nil
else
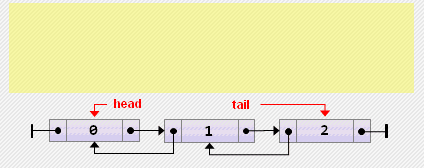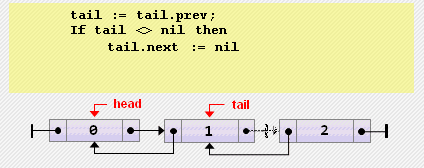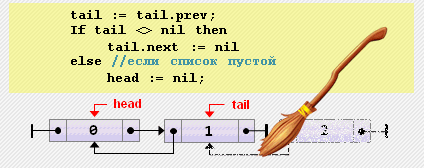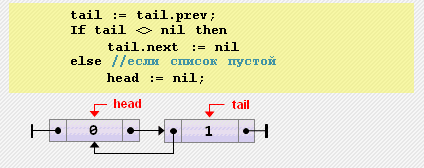
head.prev := nil;- Удаление элемента из конца
tail := tail.prev;
if tail = nil then
head := nil
else
tail.next := nil;- Вставка элемента перед текущим
if cur = head then
// вставка в начало
else
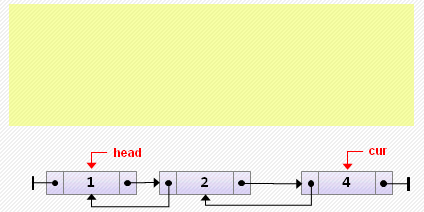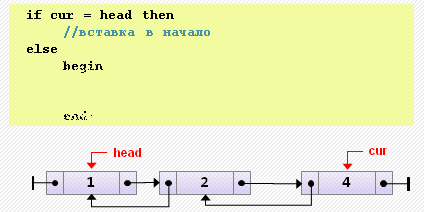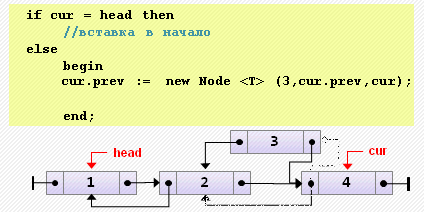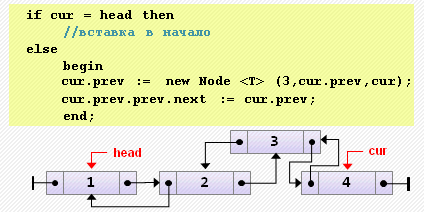
begin
cur.prev := new Node<T>(3, cur.prev, cur);
cur.prev.prev.next := cur.prev;
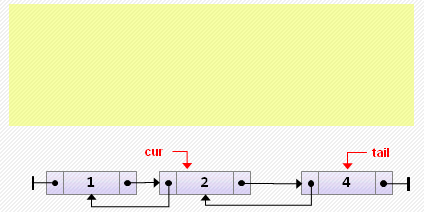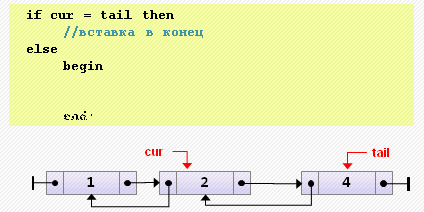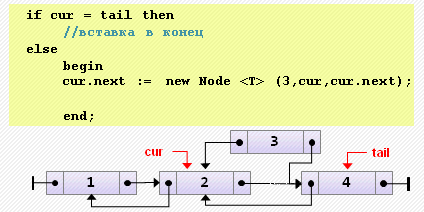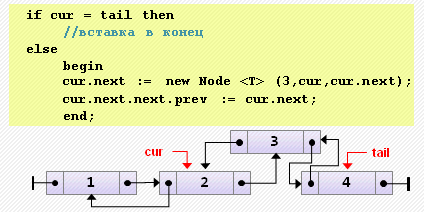
end;- Вставка элемента после текущего
if cur = tail then
// вставка в конец
else
begin
cur.next := new Node<T>(3, cur, cur.next);
cur.next.next.prev := cur.next;
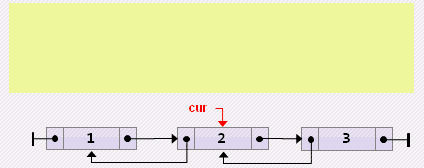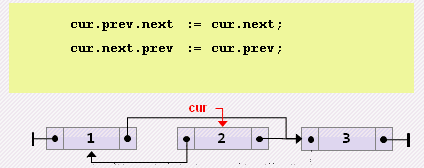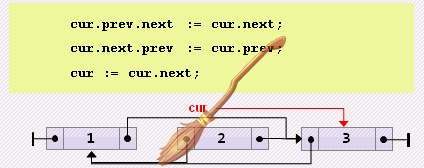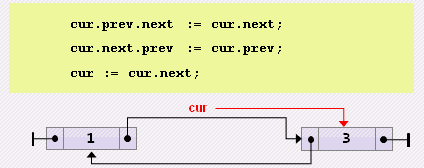
end;- Удаление текущего
if cur = head then
// удаление из начала
else if cur = tail then
// удаление из конца
else
begin
cur.prev.next := cur.next;
cur.next.prev := cur.prev;
cur := cur.next;
end;- Проход по списку
Проход по списку в прямом порядке аналогичен этой операции для односвязных списков.
Проход в обратном порядке можно организовать заменой:
- head на tail
- next на prev
Класс двусвязного линейного списка - устарело, на лекции не даю - громоздко и надо пользоваться стандартным
Ясно, что удобно оформить все операции в виде подпрограмм. Но тогда каждый раз в качестве параметров надо передавать ссылки на начало и конец списка.
Создадим класс двусвязный линейный список, полями которого будут head и tail:
type
Node<T> = class
data: T;
prev, next: Node<T>;
constructor (d: T; p, n: Node<T>);
begin
data := d;
prev := p;
next := n;
end;
end;
DoubleLinkedList<T> = class
head, tail: Node<T>;
constructor;
begin
head := nil;
tail := nil;
end;
procedure AddFirst(d: T);
begin
head := new Node<T>(d, nil, head);
if head.next <> nil then
head.next.prev := head
else // если список был пуст
tail := head;
end;
procedure AddLast(d: T);
begin
tail := new Node<T>(d, tail, nil);
if tail.prev <> nil then
tail.prev.next := tail
else // если список был пуст
head := tail;
end;
procedure DeleteFirst;
begin
head := head.next;
if head = nil then
tail := nil
else
head.prev := nil;
end;
procedure DeleteLast;
begin
tail := tail.prev;
if tail = nil then
head := nil
else
tail.next := nil;
end;
procedure InsertBefore(cur: Node<T>; d: T);
begin
if cur = head then
AddFirst(d)
else
begin
cur.prev := new Node<T>(d, cur.prev, cur);
cur.prev.prev.next := cur.prev;
end;
end;
procedure InsertAfter(cur: Node<T>; d: T);
begin
if cur = tail then
AddLast(d)
else
begin
cur.next := new Node<T>(d, cur, cur.next);
cur.next.next.prev := cur.next;
end;
end;
function RemoveAt(cur: Node<T>): Node<T>;
begin
if cur = head then
begin
DeleteFirst;
Result:=head;
end
else if cur = tail then
begin
DeleteLast;
Result:=nil;
end
else if cur = tail then
begin
DeleteLast;
result := nil;
end
else
begin
cur.prev.next := cur.next;
cur.next.prev := cur.prev;
result := cur.next;
end;
end;
procedure Print;
begin
var cur := head;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.next;
end;
end;
procedure PrintReverse;
begin
var cur := tail;
while cur <> nil do
begin
writeln(cur.data);
cur := cur.prev;
end;
end;
end;Пример.
Дан двусвязный линейный список с целыми значениями.
Удалить все его отрицательные элементы.
var list: DoublyLinkedList<integer>;
// создание списка
var cur := list.head;
while cur <> nil do
if cur.data < 0 then
cur := list.RemoveAt(cur)
else
cur := cur.next;Сравнение списков и массивов
по количеству операция (n - кол-во элементов)
| Массив | Список | |
|---|---|---|
| Вставка в конец, удаление из конца | <math>\Theta (1)</math> | <math>\Theta (1)</math> |
| Вставка в начало, удаление из начала | <math>\Theta (n)</math> | <math>\Theta (1)</math> |
| Вставка в середину, удаление из середины | <math>\Theta (n)</math> | <math>\Theta (1)</math> |
| Проход | <math>\Theta (n)</math> | <math>\Theta (n)</math> |
| Доступ по индексу | <math>\Theta (1)</math> | <math>\Theta (i)</math> |
| Поиск | <math>\Theta (n)</math> | <math>\Theta (n)</math> |