Основы программирования — Осенний семестр; Михалкович С.С.; 2008; III

Материал из Вики ИТ мехмата ЮФУ
Версия от 14:00, 21 сентября 2013; Admin (обсуждение | вклад) (→‎Примеры использования циклов)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

К основной странице курса

Циклы

Циклы с предусловием (while) и постусловием (repeat)

<xh4> Синтаксис цикла while </xh4> 

while <условие> do   <— заголовок цикла
  <оператор>   <— тело цикла

<условие>::= <логическое выражение>

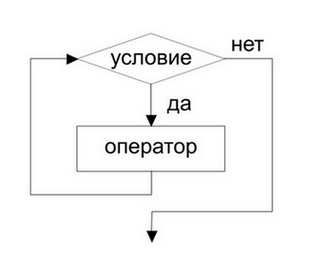
<xh4> Семантика цикла while </xh4> Цикл while м.png

<xh4> Синтаксис цикла repeat </xh4> 

repeat
  <операторы>
until <условие>

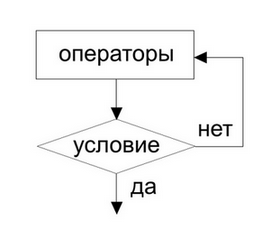
<xh4> Семантика цикла repeat </xh4> Цикл repeat м.png

Зацикливание

Зацикливание происходит, если:

  • условие цикла с предусловием всегда истинно

Пример. 

while true do
  <оператор>
  • условие цикла с постусловием всегда ложно

Пример. 

repeat
  <операторы>
until false

Итерация — однократное повторение тела цикла.

<xh4> Отличия между циклами while и repeat </xh4> while

тело может не выполниться ни разу

repeat

тело выполнится хотя бы один раз

<xh4> Примеры </xh4> Пример 1. Сумма нечетных двузначных чисел

С использованием while 

s := 0; 
x := 11;
while x < 100 do
begin
  s += x;
  x += 2;
end;

С использованием repeat 

s := 0; x := 11;
repeat
  s += x;
  x += 2;
until x = 99;

Пример 2. Факториал

С использованием repeat 

var n: integer;
read(n);
var x := n;
var p := 1;

repeat
  p *= x;
  x -= 1;
until x = 1;

С использованием while 

var n: integer;
read(n);
var x := n;
var p := 1;

while x > 1 do
begin
  p *= x;
  x -= 1;
end;

Моделирование repeat с помощью while

repeat             Op
  Op       ——>     while not A do
until A;           begin
                     Op
                   end;

Моделирование while с помощью repeat

while A do         if A then
  Op         ——>     repeat
                       Op
                     until not A

Оператор цикла с параметром (for)

<xh4> Синтаксис </xh4> 

<заголовок цикла>
  <тело цикла>

<заголовок цикла> ::= for <переменная>:=<выражение1> <направление> <выражение2> do
<тело цикла> ::= <оператор> 
<направление> ::= to | downto

<xh4> Семантика </xh4> 

var b := <выражение1>;
var e := <выражение2>;
  <переменная> := b;
 
while <переменная> <> e do
begin
  <оператор>
  <получить следующее значение переменной>
end;
<получить следующее значение переменной> ::= <переменная> += 1; | <переменная> -= 1;

<xh4> Ограничения: </xh4>

  • выражения 1 и 2 должны быть совместимы по присваиванию с переменной
  • переменная должна иметь порядковый тип (такой же, как и в case — целый, символьный или перечислимый)
  • переменная цикла for не должна меняться внутри цикла for
  • переменная цикла for должна быть описана в той же п/п, где используется цикл

Дополнительные возможности PascalABC.NET

Возможно описание переменной цикла в его заголовке: 

for [var] i: integer := 1 to 5 do
  <оператор>

Возможно автоопределение типа при описании: 

for var i := 1 to 5 do
  <оператор>

Переменная цикла, описанная в заголовке цикла, определена только внутри цикла.
Замечание. Значение переменной цикла после завершения цикла не определено. Именно поэтому рекомендуется описывать переменную цикла в заголовке цикла.

Примеры использования циклов

Табулирование функции<xh4> 

</xh4>Дана f(x) на [a; b], разбитая на N частей.

Выдать таблицу значений в точках разбиения. 

var a, b: real;
var N: integer;
read(a, b, N);

assert(N <> 0);
assert(b > a);
var h := (b - a) / N;
var x:real:=h;

Дальнейшее решение с помощью for: 

for var i := 0 to N do
begin
  writelnFormat('{0,6:f2} {1,9:f4}', x, f(x));
  x += h;
end;

Дальнейшее решение с помощью while: 

var eps := h / 2;
while x < (b + eps) do
begin
  writelnFormat('{0,6:f2} {1,9:f4}', x, f(x));
  x += h;
end;

Погрешность при работе с вещественными числами

Замечание. Вещественные числа в памяти компьютера представлены приближенно. Ошибка, которая возникает при представлении вещественного числа в памяти, называется ошибкой округления Ошибка, которая возникает в результате вычислений с вещественными числами, называется вычислительной погрешностью.

Вещественные хранятся в памяти компьютера в виде M*10p, где M называется мантиссой, p - порядком. Вещественное типа real занимает 64 бита (8 байт), из которых первый бит отводится под знак порядка, следующие 11 бит хранят значение порядка, затем идет бит для знака мантиссы и оставшиеся 51 бит отводятся для хранения мантиссы.

Минимальное положительное вещественное число называется машинным эпсилон и задается константой real.Epsilon

begin 

 writeln(real.Epsilon);

end.


Вывод. Вещественные числа нельзя сравнивать на равенство, можно только на больше/меньше.

<xh4> Рекуррентные соотношения </xh4> Говорят, что последовательность данных 

x1, x2, x3,..., xn

является рекуррентной, если 

xk + 1 = f( xk ), k = 1, 2, 3...

<xh4> Вывод степеней двойки </xh4> 

var x := 1;
for var i := 1 to 10 do
begin
  writeln(x);
  x *= 2;
end;

<xh4> Последовательность Фибоначчи </xh4> <math>\begin{cases} x_1 = 1, x_2 = 1 \\ x_{k+1} = x_k + x_{k-1}\end{cases}</math> 

var a := 1;
var b := 1;
write(a, ' ', b, ' ');
for var i := 3 to 20 do
begin
  c := a + b;
  write(c, ' ');
  a := b;
  b := c;
end;

<xh4> Вычисление НОД (алгоритм Евклида) </xh4> <math>\begin{cases} x_1 = a \\ x_2 = b \\ x_{k+1} = x_{k-1} mod x_k\end{cases}</math> 

var a, b: integer;
read(a, b);
assert((a > 0) and (b > 0));
repeat
  c := a mod b;
  a := b;
  b := c;
until c = 0;
writeln(a);

<xh4> Суммирование рядов (конечных и бесконечных) </xh4>

  • <math>\sum_{i=1}^n \frac{a^i}{i!}</math>

Найдем рекуррентную связь между ai: 

x1 = a
xi = xi-1 * a / i, i = 2, 3..

read(a, n);
x := a;
s := x;
for var i := 2 to n do
begin
  x *= a / i;
  s += x;
end;
  • <math>\sum_{i=1}^\infty (-1)^i\frac{a^i}{i}</math>

Для вычисления суммы бесконечного ряда в простейшем случае используют следующий метод:

задается некоторый малый eps и сумма <math>\sum_{i=1}^\infty x_i</math> вычисляется, пока <math>|x_i| >\ eps</math>
assert((a > 0) and (a < 1));
i := 1;
s := 0;
y := -a;
repeat
  s += y / i;
  i += 1;
  y *= -a;
until abs(y / i) < eps;

<xh4> Нахождение max в последовательности чисел </xh4> 

max := - real.MaxValue; // или max := real.MinValue;
for var i := 1 to n do
begin
  read(x);
  if x > max then
    max := x;
end;

<xh4> Разложение целого числа на простые множители </xh4> Будем делить x на p, начиная с p = 2. Если делится нацело, то p — множитель, если не делится, то увеличиваем p на 1, пока x <> 1. 

read(x);
p := 2;
repeat
  if x mod p = 0 then
  begin
    write(p, ' ');
    x := x div p;
  end
  else
    p += 1;
until x = 1;

Операторы break и continue

break — оператор досрочного завершения цикла.

Break м.png

continue — оператор досрочного завершения текущей итерации цикла.

Continue м.png

Примеры использования циклов (продолжение)

<xh4> Поиск заданного значения среди введенных </xh4> Решение 1. С использованием оператора break 

var exists: boolean := false;
for var i:=1 to n do
begin
  read(x);
  if x = k then
  begin
    exists := true;
    break;
  end;
end;

Решение 2. 

var i := 1;
var exists: boolean:= false;
repeat
  read(x);
  if x = k then
    exists := true;
  i += 1;
until (i > n) or exists;

<xh4> Обработка последовательности, завершающейся нулем </xh4> Вводятся числа. Конец ввода — ноль.
Найти сумму и произведение положительных чисел. 

s := 0;
p := 1;
while True do
begin
  read(x);
  if x = 0 then
    break; 
  if x < 0 then
    continue;  //фильтр
  s += x;
  p *= x;
end;

<xh4> Вычисление значения многочлена. Схема Горнера </xh4> Необходимо вычислить <math>\ a_0x^n + a_1x^{n-1} + ... + a_{n-1}x + a_n</math> если

a0...an известны
x дано

Решение 1. 

var p := 1.0;
var s := 0.0;
for var i := 0 to n do
begin
  read(a);
  s += p * a;
  p *= x;
end;

Это решение использует 2(n + 1) умножений.

Однако есть и другое решение — схема Горнера. Оно основана на том, что
<math>\ a_0x^2 + a_1x + a_2 = ((a_0)x + a_1)x + a_2</math>

Решение 2. 

read(a);
var res: real := a;
for var i:=1 to n do
begin
  read(a);
  res *= x;
  res += a;
end;

Итого — всего n умножений.

<xh4> Поиск нуля функции на отрезке </xh4> Требуется найти корень уравнения f( x ) = 0

  • на отрезке [a; b]
  • с заданной точностью eps
  • f(x) непрерывна на этом отрезке
  • имеет на нем ровно 1 корень, т.е. f(a ) * f( b ) < 0

Эта задача решается методом половинного деления. 

assert(b > a);
var fa := f(a);
var fb := f(b);
assert(fa * fb < 0);

while b - a > eps do
begib
  var x := (b + a) / 2;
  var fx := f(x);
  if fx * fa > 0 then
  begin
    a := x;
    fa := fx;
  end
  else
    b := x;
end;

Вложенные циклы

Метод последовательной детализации

Задача. Вывести все простые числа <= n 

writeln(2);
x := 3;
while x <= n do
begin
  Если число x — простое, то
    writeln(x);
  x += 2;
end;

Метод окаймления

Задача. Вывести Ak, A = 2..10

Метод окаймления заключается в том, что что мы окаймляем данный алгоритм внешним циклом, "размораживая" некоторый параметр.

Итак, пусть A — фиксировано( "заморожено" ). 

var p := 1.0;
for var i:=1 to k do
  p *= A;
write(p);

Теперь размораживаем A: 

for A:=2 to 10 do
begin
  ...
end;

Переборные задачи

Класс задач, в которых требуется перебрать множество вариантов и выбрать несколько оптимальных по каким-то критериям.

Задача. Дано равенство: a2 + b2 = c2, a,b,c — целые
Вывести все такие тройки (a, b, c), что: a<=1000, b<=1000, c<=1000;

Решение. 

for var a:=1 to 1000 do
for var b:=1 to 1000 do
for var c:=1 to 1000 do
  if a*a + b*b = c*c then
    writeln(a, b, c);

Однако, ясно, что 

a2 + b2 = c2 <=> b2 + a2 = c2

Кроме того, c можно вычислять.

Оптимизация. 

for var a:=1 to 1000 do
  for var b:=1 to a-1 do
  begin
    var c := round(sqrt(a*a + b*b));
    if a*a + b*b = c*c then
    begin
      writeln(a, b, c);
      writeln(b, a, c);
    end;
  end;

Вывод. При наличии нескольких вложенных циклов, в первую очередь, нужно оптимизировать самый внутренний.

Источник — «http://it.mmcs.sfedu.ru/_wiki/index.php?title=Основы_программирования_—_Осенний_семестр;_Михалкович_С.С.;_2008;_III&oldid=4880»