Основы программирования — второй семестр 08-09; Михалкович С.С.; IV часть

Содержание

1 Деревья

Деревья

Деревом назовем совокупность узлов, называемых вершинами дерева, соединенных между собой ребрами, называемыми ветвями.

Количество уровней называется глубиной дерева.
Каждая вершина нижнего уровня соединяется ровно с одной вершиной предыдущего уровня.

Единственная вершина на уровне 0 называется корнем дерева.
Она не имеет вершин-предков.

Вершины, не имеющие потомков, называют листьями дерева, а совокупность всех листьев образует крону дерева.

Примеры.

Дерево папок на диске
Самый очевидный пример — генеалогическое древо
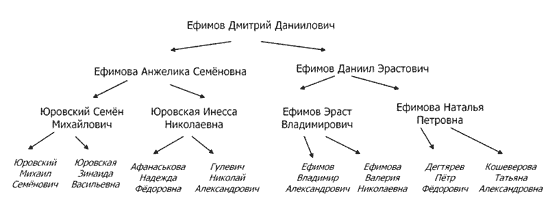
Главы и пункты книги
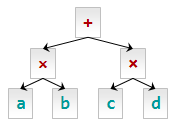
Дерево разбора выражений

a*b + c*d

Теперь дадим рекурсивное определение дерева:

Дерево ::= корень список_поддеревьев
         | ε 
Список поддеревьев ::= список_поддеревьев дерево
                     | ε
// ε означает «пусто»

Дерево называется бинарным (двоичным), если каждая его вершина имеет не более двух потомков.
(Далее бинарные деревья будем сокращать как БД)

Двоичное_дерево  ::= корень левое_поддерево правое_поддерево
                  | ε
Левое_поддерево  ::= двоичное_дерево
Правое_поддерево ::= двоичное_дерево

БД называется идеально сбалансированным, если для каждого узла количество узлов в его правом поддереве отличается от количества узлов в его левом поддереве максимум на единицу. <здесь будут рисунки деревьев>

Полным называют БД, у которого каждая вершина, не являющаяся листом, имеет ровно двух потомков, и все листья находятся на последнем уровне.

Количество узлов (u) и количество ребер (v) в произвольном дереве связаны простой формулой: <math>u = v + 1</math>.

Количество узлов в полном БД вычисляется по формуле

<math>\ 2^{n+1} - 1,</math>

где n — глубина дерева.

Доказательство

Действительно:
u₀ = 1 = 2⁰
u₁ = 2 = 2¹
u₂ = 4 = 2²
...
u_n = 2ⁿ
Значит общее количество узлов в дереве глубины n:
u(n) = 2⁰ + 2¹ + 2² + ... + 2ⁿ
Узнаем геометрическую прогрессию с n + 1 членами. А её сумма:
<math>\ S_{n+1} = b_1 \frac{q^{n+1} - 1}{q - 1} = 1 \frac{2^{n+1} - 1}{2 - 1} = 2^{n + 1} - 1</math>

Порядки обхода деревьев

Требуется составить алгоритм, обходящий все узлы дерева в некотором порядке.
Существует несколько вариантов обходов, каждый из которых описывается рекурсивным алгоритмом.

Рассмотрим эти алгоритмы для обычного и бинарного деревьев:

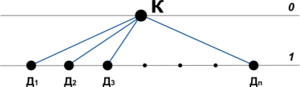
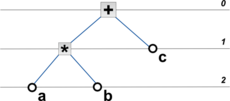
Инфиксный

Д₁ К Д₂ Д₁ К Д₃ К ... К Д_n

и

БД: Левое_поддерево Корень Правое_поддерево

Префиксный

К Д₁ Д₂ Д₁ Д₃ ... Д_n

и

БД: Корень Левое_поддерево Правое_поддерево

+ * a b c — префиксная запись выражения

Примечание. Для вычисления выражений, записанных в префиксной форме, применяется рекурсивный алгоритм.

Постфиксный

Д₁ Д₂ Д₁ Д₃ ... Д_n К

и

БД: Левое_поддерево Правое_поддерево Корень

a b * с + — обратная польская бесскобочная запись выражения

Обратная польская запись

Или Обратная польская нотация (ОПН) (Обратная бесскобочная запись (ОБЗ), Постфиксная нотация, Бесскобочная символика Лукашевича, Польская инверсная запись, Полиз) —
форма записи математических выражений, в которой операнды расположены перед знаками операций.

Обратная польская нотация была разработана австралийским философом и специалистом в области теории вычислительных машин Чарльзом Хэмблином в середине 1950-х на основе польской нотации, которая была предложена в 1920 году польским математиком Яном Лукасевичем. Работа Хэмблина была представлена на конференции в июне 1957, и издана в 1957 и 1962.

ОПН является наиболее удобной формой записи математических выражений и широко используется в вычислительной технике.
Основными её преимуществами являются возможность однократного просмотра при вычислении и простота преобразования из инфиксной записи (на основе простого алгоритма, предложенного Дейкстрой).

Подробнее см. Википедию

Реализация бинарного дерева

type
  TreeNode<T> = class
    data: T;
    left, right: TreeNode<T>;
  
    constructor (d: T; l, r: TreeNode<T>);
    begin
      data := d;
      left := l;
      right := r;
    end;
  end;

<xh4>Создание идеально-сбалансированного бинарного дерева</xh4>

type
  IntFunc = function: integer;

/// Возвращает идеально-сбалансированное дерево из n узлов
/// (Значения полей data определяются функцией GenerateInt)
function CreateTree(n: integer; GenerateInt: IntFunc): TreeNode<integer>;
begin
  if n <= 0 then
    Result := nil
  else
    Result := new TreeNode<integer>(
      GenerateInt(), 
      CreateTree((n-1) div 2, GenerateInt), 
      CreateTree(n - ((n-1) div 2) - 1, GenerateInt));
end;

function ReadInt: integer;
begin
  read(Result);
end;

function RandomInt: integer;
begin
  Result := Random(1, 99);
end;

<xh4> Обходы БД </xh4>

Инфиксный

procedure InfixPrintTree(root: TreeNode<integer>);
begin
  if root = nil then
    exit;
  
  InfixPrintTree(root.left);
  write(root.data, ' ');
  InfixPrintTree(root.right);
end;

Заметим, что кроме вывода root.data, над ним можно совершать еще массу действий (например, уменьшать на 1, или выводить его квадрат).
Поэтому есть смысл передавать в процедуру обхода выполняемое действие. Для этого определим процедурный тип и внесем в процедуру соответствующие изменения:

type
  IntAction = procedure (var data: integer);

procedure InfixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
  if root = nil then
    exit;
  
  InfixTraverseTree(root.left, Action);
  Action(root.data);
  InfixTraverseTree(root.right, Action);
end;

Префиксный

procedure PrefixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
  if root = nil then
    exit;
  
  Action(root.data);
  PrefixTraverseTree(root.left, Action);
  PrefixTraverseTree(root.right, Action);
end;

Постфиксный

procedure PostfixTraverseTree(root: TreeNode<integer>; Action: IntAction);
begin
  if root = nil then
    exit;
  
  PostfixTraverseTree(root.left, Action);
  PostfixTraverseTree(root.right, Action);
  Action(root.data);
end;

Замечание. Видим, что процедуры отличаются только моментом вызова Action. Поэтому можем избежать дублирования кода, написав процедуру, которой в качестве параметра также передается порядок обхода:

type
  /// Порядок обхода
  TraversalOrder = (Infix, Prefix, Postfix);

procedure TraverseTree(root: TreeNode<integer>; Action: IntAction; order: TraversalOrder := Infix);
begin
  if root = nil then
    exit;
  
  if order = Prefix then    // если префиксный порядок обхода, 
    Action(root.data);      // то сначала обрабатываем корень

  TraverseTree(root.left, Action, order);

  if order = Infix then     // если инфиксный, то корень надо обработать
    Action(root.data);      // после левого поддерева, но перед правым

  TraverseTree(root.right, Action, order);

  if order = Postfix then   // и если порядок постфиксный,
    Action(root.data);      // то корень обрабатывается последним
end;

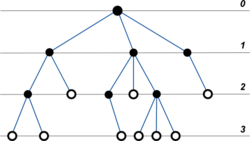
<xh4> Связь деревьев и рекурсии </xh4> Пусть у нас есть такое бинарное дерево:

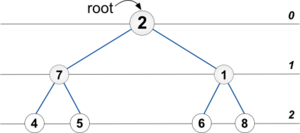
Вызовем процедуру InfixPrintTree(root).
Заметим, что её дерево рекурсивных вызовов совпадет с нашим деревом:

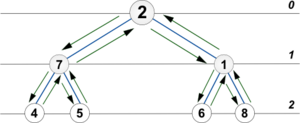
С ним же совпадет и дерево рекурсивных вызовов каждой из процедур: InfixPrintTree, PrefixPrintTree или PostfixPrintTree.

Сделаем несколько замечаний:

Форма дерева рекурсивных вызовов не зависит от порядка обхода.
В каждый момент времени глубина рекурсии совпадает с текущей глубиной дерева.
Стрелочки вниз соответствуют рекурсивному спуску, а стрелочки вверх — рекурсивному возврату.
Все алгоритмы на деревьях наиболее компактно записываются в рекурсивной форме.

Лекция 9

Задачи на бинарные деревья

<xh4>Поиск элемента в бинарном дереве</xh4>

function Find(root: TreeNode<integer>; k: integer): TreeNode<integer>;
begin
  if root = nil then
  begin
    Result := nil;
    exit;
  end;

  if root.data = k then  // если нашли элемент, то возвращаем его и прекращаем поиск
  begin                  
    Result := root;
    exit;              
  end;

  // ищем элемент в левом поддереве
  Result := Find(root.left, k);

  // если не нашли в левом поддереве, то ищем в правом
  if Result = nil then             
    Result := Find(root.right, k);
end;

Примечание. Если в списке находятся несколько искомых элементов, то будет возвращена ссылка на первый из них, а именно — находящийся в «самом левом» поддереве.

Бинарные деревья поиска

Бинарное дерево называют бинарным деревом поиска (БДП), если для каждого узла дерева выполнено следующее:
все элементы, находящиеся в левом поддереве, меньше элемента в корне, а все элементы, находящиеся в правом поддереве — больше.

Замечание. При такой формулировке определения, БДП не имеет повторяющихся элементов и называется бинарным деревом поиска без повторяющихся элементов.
А если в определении заменить все строгие неравенства на нестрогие, то БДП будет называться бинарным деревом поиска с повторяющимися элементами.

Пример БДП:

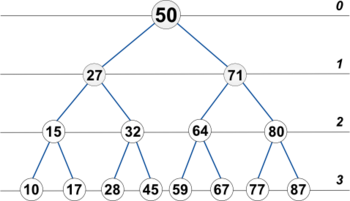
Обойдем наше БДП с помощью инфиксного обхода:

10 15 17 27 28 32 45 50 59 64 67 71 77 80 89

Значит, при инфиксном обходе БДП получаем отсортированную последовательность данных.
Т.о., в каждый момент времени БДП хранит отсортированные данные.

Каково же количество действий при обходе БДП?
Поскольку при обходе мы проходим по каждому ребру дважды (один раз — вниз, на рекурсивном спуске, и один раз — вверх, на рекурсивном возврате), то мы тратим количество действий, в два раза превышающее количество ребер.
Т.к. количество ребер на 1 меньше количества вершин, то всего тратится <math>2(n - 1)</math> действий, где <math>n</math> — количество вершин (для сравнения: в массиве обход занимает <math>n</math> действий.

<xh4>Алгоритм добавления элемента к БДП</xh4> Алгоритм добавления элемента к БДП с повторяющимися элементами будет немного отличаться от алгоритма добавления к БДП без повторяющихся элементов — во втором случае, если элемент, который мы хотим добавить, в дереве уже есть, мы ничего не делаем.
Этот случай и рассмотрим:

procedure Add(var root: TreeNode<integer>; x: integer);
begin
  if root = nil then
  begin
    root := new TreeNode<integer>(x, nil, nil);
    exit;
  end;

  if x < root.data then
    Add(root.left, x)
  else if x > root.data then
    Add(root.right, x);
end;

Теперь создание дерева не представляет сложности:

var n := 15;
var r: TreeNode<integer> := nil;

for var i := 1 to n do   // создание случайного БДП с количеством вершин, равным n
  Add(r, Random(100));

Вспомним, что при инфиксном выводе БДП получаем отсортированную последовательность данных, значит при n вызовах процедуры добавления элемента к БДП, получим отсортированную последовательность из n элементов.
Поэтому данный алгоритм называется алгоритмом сортировки деревом.

Разберемся, сколько действий потребует одно добавление в среднем.
Пусть дерево, в которое мы добавляем, является идеально-сбалансированным, тогда количество его уровней <math>k \approx \; log_2 n</math>, где <math>n</math> — количество узлов.
Видим, что количество операций в Add совпадает глубиной дерева <math>k</math> (при каждом рекурсивном вызове Add мы опускаемся вниз по дереву на 1 уровень, и вставка осуществляется в лист дерева)

Т.о., при добавлении <math>n</math> элементов, в случае, если дерево всякий раз остается близким к идеально-сбалансированному, тратится <math>n\log_2 n</math> действий (столько же, сколько при быстрой сортировке).

Замечание 1. Данная оценка справедлива в среднем.
Замечание 2. Данная оценка совпадает с оценкой количества операций при быстрой сортировке, а значит является оптимальной для произвольных данных.

<xh4>Оценка количества операций при сортировке деревом в худшем случае</xh4> Будем добавлять элементы в БДП в возрастающем порядке:

Add(10);
Add(15);
Add(17);
...
Add(87);

Получим "однобокое" дерево:

При таком порядке добавлений, количество операций составляет примерно <math>n^2</math> (как и в худшем случае быстрой сортировки).

Замечание. Чтобы сохранить асимптотическую оценку <math>n\log_2 n</math> и в худшем случае, всякий раз, при добавлении в дерево, надо проводить так называемую перебалансировку, которая сохраняет свойство дерева быть деревом поиска, но уменьшает, по возможности, его глубину до минимальной.

<xh4>Поиск элемента в БДП</xh4>

function Find(root: TreeNode<integer>; x: integer): boolean;
begin
  if root = nil then
    Result := false
  else if root.data = x then
    Result := True
  else if x < root.data then 
    Result := Find(root.left, x) 
  else // if x > root.data then 
    Result := Find(root.right, x);
end;

Очевидно, количество операций совпадает с глубиной БДП <math>k \approx \; log_2 n</math> в среднем.
Заметим, что алгоритм бинарного поиска в отсортированном массиве занимает столько же действий.

Основы программирования — второй семестр 08-09; Михалкович С.С.; IV часть

Содержание

Деревья

Порядки обхода деревьев

Реализация бинарного дерева

Задачи на бинарные деревья

Бинарные деревья поиска

Навигация

Просмотры

Персональные инструменты

Навигация

Поиск

Инструменты