Основы программирования — второй семестр 08-09; Михалкович С.С.; IV часть

Лекция 8

Деревья

Деревом назовем совокупность узлов, называемых вершинами дерева, соединенных между собой ребрами, называемыми ветвями.

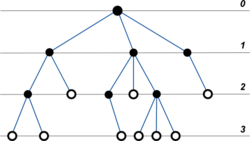
Количество уровней называется глубиной дерева.
Каждая вершина нижнего уровня соединяется ровно с одной вершиной предыдущего уровня.

Единственная вершина на уровне 0 называется корнем дерева.
Она не имеет вершин-предков.

Вершины, не имеющие потомков, называют листьями дерева, а совокупность всех листьев образует крону дерева.

Примеры.

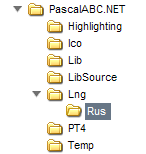
• Дерево папок на диске
  
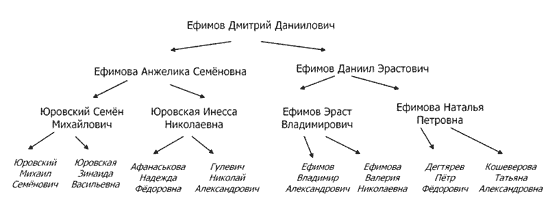
• Самый очевидный пример — генеалогическое древо
  
• Главы и пункты книги
  
• Дерево разбора выражений

a*b + c*d

Теперь дадим рекурсивное определение дерева:

Дерево ::= корень список_поддеревьев
         | ε 
Список поддеревьев ::= список_поддеревьев дерево
                     | ε
// ε означает «пусто»

Дерево называется бинарным (двоичным), если каждая его вершина имеет не более двух потомков.
(Далее бинарные деревья будем сокращать как БД)

Двоичное_дерево  ::= корень левое_поддерево правое_поддерево
                  | ε
Левое_поддерево  ::= двоичное_дерево
Правое_поддерево ::= двоичное_дерево

БД называется идеально сбалансированным, если для каждого узла количество узлов в его правом поддереве отличается от количества узлов в его левом поддереве максимум на единицу. <здесь будут рисунки деревьев>

Полным называют БД, у которого каждая вершина, не являющаяся листом, имеет ровно двух потомков, и все листья находятся на последнем уровне.

Нетрудно заметить, что количество узлов (u) и количество ребер (v) связаны простой формулой: <math>u = v + 1</math>.

Количество узлов в полном БД высчитывается по формуле
<math>\ 2^{n+1} - 1</math>

Доказательство  

Действительно:
u₀ = 1 = 2⁰
u₁ = 2 = 2¹
u₂ = 4 = 2²
...
u_n = 2ⁿ
Значит общее количество узлов в дереве глубины n:
u(n) = 2⁰ + 2¹ + 2² + ... + 2ⁿ
Узнаем геометрическую прогрессию с n + 1 членами. А её сумма:
<math>\ S_{n+1} = b_1 \frac{q^{n+1} - 1}{q - 1} = 1 \frac{2^{n+1} - 1}{2 - 1} = 2^{n + 1} - 1</math>

Порядки обхода деревьев

Требуется составить алгоритм, обходящий все узлы дерева в некотором порядке.
Существует несколько вариантов обходов, каждый из которых описывается рекурсивным алгоритмом.

Рассмотрим эти алгоритмы для обычного и бинарного деревьев:
   

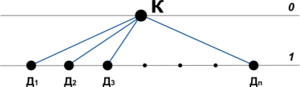
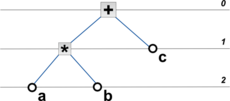
• Инфиксный

Д₁ К Д₂ Д₁ К Д₃ К ... К Д_n

и

БД: Левое_поддерево Корень Правое_поддерево

• Префиксный

К Д₁ Д₂ Д₁ Д₃ ... Д_n

и

БД: Корень Левое_поддерево Правое_поддерево

+ * a b c — префиксная запись выражения

Примечание. Для вычисления выражений, записанных в префиксной форме, применяется рекурсивный алгоритм.

• Постфиксный

Д₁ Д₂ Д₁ Д₃ ... Д_n К

и

БД: Левое_поддерево Правое_поддерево Корень

a b * с + — обратная польская бесскобочная запись выражения

Обратная польская запись  

Или Обратная польская нотация (ОПН) (Обратная бесскобочная запись (ОБЗ), Постфиксная нотация, Бесскобочная символика Лукашевича, Польская инверсная запись, Полиз) —
форма записи математических выражений, в которой операнды расположены перед знаками операций.

Обратная польская нотация была разработана австралийским философом и специалистом в области теории вычислительных машин Чарльзом Хэмблином в середине 1950-х на основе польской нотации, которая была предложена в 1920 году польским математиком Яном Лукасевичем. Работа Хэмблина была представлена на конференции в июне 1957, и издана в 1957 и 1962.

ОПН является наиболее удобной формой записи математических выражений и широко используется в вычислительной технике.
Основными её преимуществами являются возможность однократного просмотра при вычислении и простота преобразования из инфиксной записи (на основе простого алгоритма, предложенного Дейкстрой).

Подробнее см. Википедию

Реализация бинарного дерева

type
  TreeNode<T> = class
    data: T;
    left, right: TreeNode<T>;
  
    constructor (d: T; l, r: TreeNode<T>);
    begin
      data := d;
      left := l;
      right := r;
    end;
  end;

<xh4>Создание идеально-сбалансированного бинарного дерева</xh4>

type
  IntFunc = function: integer;

/// Возвращает идеально-сбалансированное дерево из n узлов
/// (Значения полей data определяются функцией GenerateInt)
function CreateTree(n: integer; GenerateInt: IntFunc): TreeNode<integer>;
begin
  if n <= 0 then
    Result := nil
  else
    Result := new TreeNode<integer>(
      GenerateInt(), 
      CreateTree((n-1) div 2, GenerateInt), 
      CreateTree(n - ((n-1) div 2) - 1, GenerateInt));
end;

function ReadInt: integer;
begin
  read(Result);
end;

function RandomInt: integer;
begin
  Result := Random(1, 99);
end;

<xh4> Обходы БД </xh4>

<xh4> Связь деревьев и рекурсии </xh4>

Лекция 9

Задачи на бинарные деревья

Класс TreeNode<T>

Создание идеально сбалансированного дерева.

Вывод узлов дерева в инфиксном, префиксном, постфиксном порядке.

Связь деревьев и рекурсии.

Определение глубины дерева.

Количество листов в дереве.

Поиск элемента в дереве.

Бинарные деревья поиска

Определение БДП.

Добавление в БДП. Инвариантность БДП относительно операции добавления.

Оценка количества операций при добавлении. Худший случай.

Сортировка деревом. Асимптотическая сложность алгоритма.

Поиск элемента в БДП.

Произвольные деревья

TreeNode = class
  data: integer;
  leftChild, rightSibling: TreeNode;
end;

function CreateRandomTree(n: integer; m: integer): TreeNode;  
// n - количество сыновей, m - количество уровней
begin
  Result := nil;
  if m=0 then exit;
  for var i:=1 to n do
    Result := new TreeNode(Random(100), CreateRandomTree(Random(1,5), m-1), Result)
end;

root := CreateRandomTree(3,4);
root := new TreeNode(Random(100), root, nil);

procedure PrintTree(r: TreeNode);
begin
  while r<>nil do
  begin
    write(r.data,' ');
    PrintTree(r.leftChild);
    r := r.rightSibling;
  end
end;