Конспект лекций «Методы построения компиляторов» — различия между версиями

Текущая версия на 11:16, 11 сентября 2017

К основной странице курса

Содержание

1 Литература
2 Лекция 1
- 2.1 Введение в компиляцию
  - 2.1.1 Разновидности компиляторов
  - 2.1.2 Фазы компиляции
3 Лекция 2
4 Порождающие грамматики
5 Перевод (трансляция)
6 Синтаксический анализ
- 6.1 Нисходящий синтаксический анализ
  - 6.1.1 Нерекурсивный предиктивный анализ
  - 6.1.2 Множества FIRST и FOLLOW
- 6.2 Восходящий синтаксический анализ
7 Генераторы лексических и синтаксических анализаторов
- 7.1 Создание лексического анализатора (сканера) с помощью gplex
- 7.2 Создание синтаксического анализатора с помощью gppg

Литература

Ахо А., Сети Р., Ульман Д. Компиляторы. Принципы, технологии, инструменты. — М.: Вильямс, 2001.
Карпов Ю. Г. Основы построения трансляторов. — М.: BHV, 2005.
Свердлов С. З. Языки программирования и методы трансляции. — М.: Питер, 2007.
Опалева Э. А., Самойленко В.П. Языки программирования и методы трансляции. — М.: BHV, 2005.

Лекция 1

Введение в компиляцию

Что такое компилятор. Исходный и целевой язык.

Разновидности компиляторов

Интерпретаторы
Форматтеры текста
Статические анализаторы кода
Препроцессоры
- макросы define
- включение файлов #include
- условная компиляция #ifdef
- расширения языка, которые препроцессор переводит в код на языке

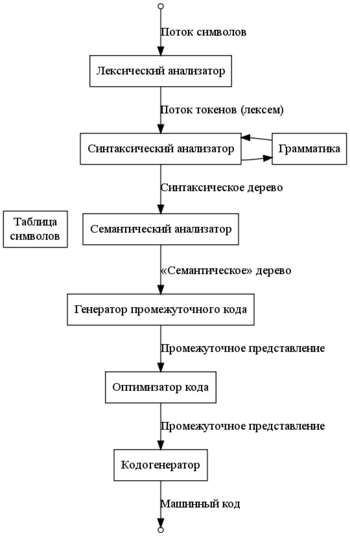
Фазы компиляции

Лексический анализ (сканирование)
Синтаксический анализ (разбор, „парсинг“)
Семантический анализ

На примере выражения p := i + r * 60

 id1 := id2 + id3 * 60

Обнаружение ошибок. Лексические, синтаксические и семантические ошибки.
Генерация промежуточного кода

На примере трехадресного кода

 t1 := IntToReal(60)
 t2 := id3 * t1;
 t3 := id2 + t2;
 id1 := t3;

Оптимизация кода

 t1 := id3 * 60.0;
 id1 := id2 + t1;

Генерация кода (основное - назначение переменных регистрам)

 MOVF id3, R2
 MULF #60.0, R2
 MOVF id2, R1
 ADDF R2, R1
 MOVF R1, id1

Почти на каждой стадии могут выполняться дополнительные оптимизации, а также происходит анализ и обработка ошибок.

Математическим обеспечением фаз лексического и синтаксического анализа является теория формальных языков. Обычно лексические анализаторы генерируются с помощью регулярных выражений.

Синтаксический анализ основывается на теории контекстно-свободных (КС) грамматик. Общая форма КС-грамматики не позволяет разбирать язык достаточно простым (в частности, автоматически сгенерированным) парсером, потому языки программирования обычно принадлежат одному из нескольких специальных подклассов КС-языков (LL, LR, LALR), которые проще разбирать и некоторые из которых будут подробно изучены в курсе.

Упомянутые достижения теории формальных языков насчитывают уже несколько десятков лет, и в этой области не ожидается каких-либо новых разработок, тем более что имеющиеся теоретические результаты хорошо решают практические задачи. По другому обстоит дело с изучением других двух разделов компиляции: семантическим анализом и оптимизацией. Работы по формальному описанию семантики языков программирования интенсивно появлялись в 70–80-х годах. Однако ни одна из построенных теорий не вошла в широкое употребление при построении компиляторов, и сегодня дело обстоит таким образом, что семантика вначале описывается на естественном языке, а затем реализуется в компиляторе большим набором вручную закодированных условных операторов.

Напротив, в последние годы растёт актуальность теории оптимизирующих преобразований — это объясняется появлением всё более высокоуровневых языков и разнообразных аппаратных платформ. Оптимизация также требует привлечения развитого математического аппарата (в частности, для решения вопроса о корректности преобразований). Многие из достижений активно внедряются в промышленные компиляторы. Всё больше это касается преобразований, связанных с распараллеливанием.

На этапе построения семантического дерева строится таблица символов - в нее заносятся имена, присутствовавшие в исходном тексте, к ним добавляются такие атрибуты как тип, отведённая память, область видимости.

Лекция 2

Группировка фаз

Front-end и back-end компиляторы.

Перечисленные выше фазы обычно группируются в два модуля — front-end и back-end, в зависимости от того, к какой стороне процесса компиляции они ближе, к исходному языку или к машинному коду для целевой платформы, соответственно. Возможность отдельно разрабатывать front-end и back-end повышает эффективность труда разработчиков компиляторов — насколько, зависит от эффективности используемого внутреннего представления, связывающего эти два модуля. В последнее время всё чаще выделяют middle-end — части компилятора, активно работающие с промежуточным представлением.

Проходы. Группировка фаз компилятора в проходы (например, объединение фаз лексического, синтаксического, семантического анализа и генерации кода).

Разбиение процесса компиляции на фазы является логическим. Есть и другой, физический подход к такому разбиению — на проходы. Проходом обычно считается одно чтение исходного потока (и, возможно, одна законченная генерация выходного). Разные фазы могут группироваться в один проход.

Уменьшение количества проходов (на примере предварительного описания подпрограмм). Технология обратных поправок.

Компиляция и многомодульность. Необходимость компилировать модуль в некоторый формат, содержащий правильную программу. Перемещаемые адреса. Редактор связей (линковщик).

Инструментарий для создания компиляторов

Генераторы лексических анализаторов (сканеров)
Генераторы синтаксических анализаторов (парсеров)
Автоматические генераторы кода

Компиляторы компиляторов

Lex + Yacc
Flex + Bison
CoCo
Antlr
Gold Parser Builder
GPLex + GPPG

Порождающие грамматики

Определение. Символы: терминалы и нетерминалы. Продукции (правила вывода). Стартовый символ.

Обозначения

a,b,c, ... - терминалы
u,v,w,x,y,z - строки (цепочки) терминалов
A,B,C, ... - нетерминалы
α,β,γ, ... - строки (цепочки) нетерминалов и терминалов
ε - пустая цепочка

Опр. формальной грамматики (порождающей грамматики Хомского)

G = (N,Σ,P,S)
N - нетерминалы
Σ - терминалы
P - правила вывода (продукции) вида α→β, α - непустая

V = Σ + N - множество всех нетерминалов и терминалов

X^* - множество всех цепочек символов из X

X⁺ = X^* - {ε}

Классификация формальных грамматик по Хомскому (1956 г.)

Грамматика типа 0 (общего вида). Правила имеют вид α→β
Грамматика типа 1 (контекстно зависимая, КЗ)

Правила имеют вид αAβ → αγβ. γ принадлежит V⁺, т.е. грамматика является неукорачивающей

Добавляется также правило S → ε

α,β называются левым и правым контекстом

Грамматика типа 2 (контекстно свободная, КС)

Правила имеют вид A → α. α ∊ V*

Наиболее близкая к БНФ

Грамматика типа 3 (автоматная, регулярная)

Правила имеют вид A → aB, A → a, A → ε (правая регулярная грамматика)

Автоматные языки содержатся в КС языках

Пример. Грамматика, порождающая язык правильных скобочных выражений.

S → (S) | SS | ε

Порождение (вывод)

Далее будем говорить только о КС-грамматиках.

Грамматика G порождает (выводит) цепочки из стартового символа, используя правила вывода.

Пример.

S => (S) => (SS) => ((S)S) => (()S) => (()(S)) => (()())

Обозначения

α =>_lm β   - левый вывод
α =>_* β  - 1 или более шагов вывода
α =>₊ β  - 0 или более шагов вывода

Опр. Сентенциальной формой грамматики называется строка, которая может быть выведена из стартового символа.

Опр. Предложением (сентенцией) грамматики называется сентенциальная форма, состоящая из одних терминалов.

Опр. Языком над алфавитом (словарём) Σ называется подмножество L множества Σ^*.

Опр. Языком L(G), порождаемым грамматикой G, называется множество всех ее предложений:

L(G) = { w | w ∊ Σ^*, S =>* w }

Опр. Две грамматики называются эквивалентными, если языки, ими порождаемые, совпадают:

G₁ ~ G₂ <=> L(G₁) = L(G₁)

Утв. Проблема эквивалентности КС-грамматик алгоритмически неразрешима.

Левый, правый вывод (порождение). Деревья вывода (разбора)

Опр. Если в процессе вывода заменяется всякий раз самый левый нетерминал, то такой вывод называется левым.

Пример

E → E + T
  | T
T → T * F
  | F
F → i
  | ( E )

Левый и правый вывод для предложения i + i * i

Дерево вывода (дерево разбора) строки предложения. В отличие от порождения, из него исключена информация о порядке вывода.

Крона дерева разбора - цепочка меток листьев слева направо

Неоднозначные грамматики

Грамматика, которая дает более одного дерева разбора для некоторого предложения, называется неоднозначной.

Пример неоднозначной грамматики. Грамматика арифметических выражений.

E → E+E | E*E | i

Два дерева разбора для цепочки i + i * i

Преобразование в эквивалентную однозначную грамматику:

E → E + T
  | T
T → T * P
  | P
P → i

Пример неоднозначной грамматики. Грамматика условного оператора

S → if b then S
  | if b then S else S
  | a

Два дерева разбора для цепочки if b then if b then a

Преобразование в эквивалентную однозначную грамматику:

S → if b then S
  | if b then S2 else S
  | a  
S2 → if b then S2 else S2
  | a

Утверждение. Проблема неоднозначности произвольной КС-грамматики алгоритмически не разрешима

Леворекурсивные грамматики, их проблемы. Алгоритм устранения левой рекурсии.

Перевод (трансляция)

Ранее мы решали вопрос о принадлежности некоторой цепочки α интересующему нас языку L, задаваемому грамматикой G. Но задача компиляции шире: не только распознать входную цепочку, но и сгенерировать выходную.

Определение. Пусть Σ и Δ — два алфавита (называемые „входным“ и „выходным“ соответственно). L₁ ⊂ Σ*, L₂ ⊂ Δ*. Переводом с языка L1 на язык L2 называется отображение τ: L1 → L2.

Чтобы решить указанную задачу (т.е. конструктивно определить перевод), можно встроить в процесс проверки принадлежности некоторые действия, формирующие на выходе желаемый результат.

Схема синтаксически управляемого перевода (СУ-схема)

Неформальное определение. СУ-схема это грамматика, в которую с каждым синтаксическим правилом встроен элемент перевода.

Пример. Перевод алгебраического выражения в ПОЛИЗ (польская инверсная запись). Запишем правила грамматика вместе с элементами перевода.

Правило	Элемент перевода
E → E + T	E = E T +
E → T	E = T
T → T * P	T = T P *
T → P	T = P
P → (E)	P = E
P → <id>	P = <id>

Выведем цепочку a * (b + c) и одновременно переведём её в ПОЛИЗ: a b c + * (как обычно, используем левый вывод):

(E, E) ⇒ (T, T) ⇒ (T * P, T P *) ⇒ (P * P, P P *) ⇒ (a * P, a P *) ⇒ (a * (E), a E *) ⇒
       ⇒ (a * (E + T), a E T + *) ⇒* (a * (b + c), a b c + *)

Определение. Схема синтаксически управляемого перевода это пятёрка

T = (N, Σ, Δ, R, S),

где:

N — множество нетерминалов („переменных“),
Σ — входной алфавит,
Δ — выходной алфавит,
S — стартовый символ (S ∊ N),
R = {A → (α, β) | A ∊ N, α ∊ (N ∪ Σ)*, β ∊ (N ∪ Δ)*}.

Причём α и β в каждом конкретном правиле содержат одни и те же нетерминалы с точностью до перестановки.

Далее считаем, что задана некоторая СУ-схема T = (N, Σ, Δ, R, S).

Определение. Входная грамматика, соответствующая СУ-схеме T, это четвёрка

G_in = (N, Σ, R, S),

где

P = {A → α | ∃β A → (α, β) ∊ R}.

Определение. Выходная грамматика, соответствующая СУ-схеме T, это четвёрка

G_o = (N, Δ, R, S),

где

P = {A → β | ∃α A → (α, β) ∊ R}.

Определение. СУ-перевод (СУ-трансляция) это множество

{(x, y) | (S, S) ⇒* (x, y), x ∊ Σ*, y ∊ Δ*},

обозначаемое обычно τ(T).

СУ-перевод можно понимать как трансформацию синтаксических деревьев (соответствующих выводу входной и выходной цепочек).

Пример. ...

Транслирующие грамматики

Позволяют решать задачу перевода в более сложных случаях, чем СУ-схемы. ТГ это разновидность КС-грамматик, где символы (терминалы) разделены на два множества, Σ_i и Σ_a (a от action), называемые „входными“ и „операционными“ соответственно. При использовании ТГ, чтобы различать элементы Σ_i и Σ_a, будем заключать последние в фигурные скобки, ‘{’, ‘}’, считая получившиеся на письме три символа одним символом алфавита.

Пример. Перевод простого алгебраического выражения в ПОЛИЗ ...

Определение. Пусть α ∊ (Σ_i ∪ Σ_a)*. Тогда α называется активной цепочкой. Входные (операционные) символы активной цепочки, записанные отдельно в том же порядке, как они встречались в ней, образуют входную (операционную) цепочку.

Операционные символы можно трактовать как имена процедур, выполняющих определённые действия. Пока — процедур без параметров. Операционные символы также могут использоваться для интерпретации кода. Операционные символы могут находиться в любой части результата продукции, не только в суффиксе, но это может сильно усложнить парсер (иногда придётся откатываться).

Атрибутные грамматики и трансляция

В АГ с каждым символом грамматики может быть связан один или несколько атрибутов. Для каждого синтаксического правила вводятся семантические правила, устанавливающие функциональные зависимости между атрибутами.

Дерево, содержащее атрибуты, называется аннотированным. Атрибуты придают смысл синтаксической структуре, описываемой деревом, и потому аннотированное дерево называется также семантическим деревом.

Пример. Вычисление простого арифметического выражения ...

Типы атрибутов.

Синтезированные — значения таких атрибутов зависят только от значений атрибутов потомков в дереве разбора.
Унаследованные — значения таких атрибутов зависят от значений атрибутов родительского узла, узлов-братьев и сестёр (дочерних для родительского), а также других атрибутов самого узла.

Синтаксический анализ

Понятие синтаксического анализатора.

Нисходящие (top-down) и восходящие (bottom-up) синтаксические анализаторы

Нисходящий синтаксический анализ

Опр. Синтаксический анализатор, работающий методом рекурсивного спуска и не требующий откатов, называется предиктивным синтаксическим анализатором.

Нерекурсивный предиктивный анализ

Схема работы со стеком, таблицей разбора, входным буфером

Алгоритм нерекурсивного предиктивного анализа

Пример

Множества FIRST и FOLLOW

Определение.

Пример.

Алгоритм построения таблиц предиктивного анализа.

Определение LL(1) грамматики. Пояснение названия.

Утв. LL(1) грамматика не может быть леворекурсивной или неоднозначной.

Эквивалентное определение LL(1) грамматики.

Восстановление после ошибок в предиктивном анализе.

Восходящий синтаксический анализ

Наиболее распространенная разновидность - ПС-анализ (перенос-свертка - shift-reduce)

Понятие основы. Примеры.

Обращенное правое порождение и обрезка основ.

Стековая реализация ПС-анализа. Основные операции:

Перенос (shift)
Свертка (reduce)
Допуск  (accept)
Ошибка  (error)

Утв. Основа всегда находится на вершине стека и никогда - внутри него. Доказательство.

Понятие активного префикса.

LR-анализаторы. SLR, канонический LR и LALR анализаторы.

Общая схема и алгоритм LR-анализа. Пример.

LR-грамматики.

Неоднозначности вида shift-reduce и их разрешение.

Генераторы лексических и синтаксических анализаторов

Обзор.

Yacc, Lex
Byson, Flex
CoCo
ANTLR
Gold Parser Builder
GPPG

Создание лексического анализатора (сканера) с помощью gplex

Общая структура .l файла

Особенности .l файла gplex

Возвращение типов лексем

Лексемы идентификаторов, чисел.

Ключевые слова

Позиция лексемы

Начальные состояния сканера, их изменение, использование для вырезания комментариев:

%x COMMENT
%%
"/*" { BEGIN(COMMENT);}
<COMMENT> "*/" { BEGIN(INITIAL);}
<COMMENT> <<EOF>> { Console.WriteLine("Комментарий не закрыт");}

Создание синтаксического анализатора с помощью gppg

Общая структура .y файла

Задание типов лексем

Таблица приоритетов и ассоциативности

Особенности .y файла gppg

Примеры

Простейший калькулятор
- Простейший калькулятор с приоритетом операций
- Создание дерева разбора программы
- Преобразование в XML
- Добавление переменных. Представление о таблице символов
- Добавление присваивания
- Добавление типов
- Добавление управляющих конструкций

@@ Строка 1: / Строка 1: @@
 [[Категория:Конспекты]]
 [[Категория:Методы построения компиляторов]]
+[[Страница_курса_%22Методы_построения_компиляторов%22| К основной странице курса]]
 ==Литература==
 # {{Книга
@@ Строка 110: / Строка 112: @@
 Определение.
-Терминалы, нетерминалы, символы. Продукции. Стартовый символ.
+Символы: терминалы и нетерминалы. Продукции (правила вывода). Стартовый символ.
 Обозначения
@@ Строка 123: / Строка 125: @@
   N - нетерминалы
   Σ - терминалы
-  P - правила вида α→β
+  P - правила вывода (продукции) вида α→β, α - непустая
 V = Σ + N - множество всех нетерминалов и терминалов
-V* - множество всех цепочек символов из V
-V+ = V* - {ε}
-===Классификация формальных грамматик по Хомскому (напоминание из курса ТАиФЯ)===
+X<sup>*</sup> - множество всех цепочек символов из X
+X<sup>+</sup> = X<sup>*</sup> - {ε}
+===Классификация формальных грамматик по Хомскому (1956 г.)===
 * Грамматика типа 0 (общего вида). Правила имеют вид α→β
 * Грамматика типа 1 (контекстно зависимая, КЗ)
-: Правила имеют вид αAβ → αγβ. γ принадлежит V+, т.е. грамматика является неукорачивающей
+: Правила имеют вид αAβ → αγβ. γ принадлежит V<sup>+</sup>, т.е. грамматика является неукорачивающей
-: α,β называются левым и правым контекстом
+: Добавляется также правило S → ε
+: α,β называются '''левым и правым контекстом'''
 * Грамматика типа 2 (контекстно свободная, КС)
-: Правила имеют вид A → α. α принадлежит V*, т.е. грамматика может быть укорачивающей => КС языки не содержатся в КЗ
+: Правила имеют вид A → α. α ∊ V*
 : Наиболее близкая к БНФ
 * Грамматика типа 3 (автоматная, регулярная)
-: Правила имеют вид A → aB, A → a, a принадлежит Σ + {ε}
+: Правила имеют вид A → aB, A → a, A → ε  (правая регулярная грамматика)
 : Автоматные языки содержатся в КС языках
-Пример. Грамматика правильных скобочных выражений.
+Пример. Грамматика, порождающая язык правильных скобочных выражений.
   S → (S) | SS | ε
 ===Порождение (вывод)===
+Далее будем говорить только о КС-грамматиках.
+Грамматика G порождает (выводит) цепочки из стартового символа, используя правила вывода.
+Пример.
+ S => (S) => (SS) => ((S)S) => (()S) => (()(S)) => (()())
 Обозначения
-  =>
+  α =><sub>lm</sub> β   - левый вывод
-  =>+ (1 или более)
+  α =><sub>*</sub> β  - 1 или более шагов вывода
-  =>* (0 или более)
+  α =><sub>+</sub> β  - 0 или более шагов вывода
 Опр. '''Сентенциальной формой''' грамматики называется строка, которая может быть выведена из стартового символа.
@@ Строка 156: / Строка 168: @@
 Опр. '''Предложением''' (сентенцией) грамматики называется сентенциальная форма, состоящая из одних терминалов.
-Опр. '''Языком''' L(G) грамматики G называется множество всех ее предложений.
+Опр. '''Языком''' над алфавитом (словарём) Σ называется подмножество L множества Σ<sup>*</sup>.
-Обозначения
+Опр. '''Языком''' L(G), порождаемым грамматикой G, называется множество всех ее предложений:
-  =>(lm)
+  L(G) = { w | w ∊ Σ<sup>*</sup>, S =>* w }
-  =>(lm)*
- =>(rm)+
+Опр. Две грамматики называются эквивалентными, если языки, ими порождаемые, совпадают:
+  G<sub>1</sub> ~ G<sub>2</sub> <=> L(G<sub>1</sub>) = L(G<sub>1</sub>)
+Утв. Проблема эквивалентности КС-грамматик алгоритмически неразрешима.
+===Левый, правый вывод (порождение). Деревья вывода (разбора)===
-Левый, правый вывод (порождение).
+Опр. Если в процессе вывода заменяется всякий раз самый левый нетерминал, то такой вывод называется левым.
 Пример
   E → E + T
     | T
-  T → T * P
+  T → T * F
-    | P
+    | F
-  P → i
+  F → i
     | ( E )
 Левый и правый вывод для предложения i + i * i
-Дерево вывода (синтаксическое дерево, дерево разбора) строки предложения. В отличие от порождения, из него исключена информация о порядке вывода.
+Дерево вывода (дерево разбора) строки предложения. В отличие от порождения, из него исключена информация о порядке вывода.
 Крона дерева разбора - цепочка меток листьев слева направо
+===Неоднозначные грамматики===
 Грамматика, которая дает более одного дерева разбора для некоторого предложения, называется '''неоднозначной'''.